The_Thinker
- 145
- 2
A bit weird magnetism problem...
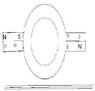
You see i have a problem... Assume the below situation in which there are 4 magnets above a wire and connected to a wheel of some sort. Now, once the wheel is in motion, Each set of the magnets have one strong and one weak magnet. In the first set, the strong magnet which is placed first, has north nearer to the wire than its south and in the weaker magnet the south nearer to the wire than the north. In the second set, its just the opposite... It's clear from the picture attached...Now the question is, if the wheel is put into motion... what is the resultant magnitude of the magnetic field with the wire in each turn that the magnets come near it and is there any current induced... if so what is it and finally if there is damping... what is it? The answer is asked only in terms of mathematical formulae...
I'm clueless...
P.S.
I'm sorry abt the picture quality... but i had real tough time uploading it... the file size was too large..., the picture was too big... eitherway.. i finally got it done...
You see i have a problem... Assume the below situation in which there are 4 magnets above a wire and connected to a wheel of some sort. Now, once the wheel is in motion, Each set of the magnets have one strong and one weak magnet. In the first set, the strong magnet which is placed first, has north nearer to the wire than its south and in the weaker magnet the south nearer to the wire than the north. In the second set, its just the opposite... It's clear from the picture attached...Now the question is, if the wheel is put into motion... what is the resultant magnitude of the magnetic field with the wire in each turn that the magnets come near it and is there any current induced... if so what is it and finally if there is damping... what is it? The answer is asked only in terms of mathematical formulae...
I'm clueless...
P.S.
I'm sorry abt the picture quality... but i had real tough time uploading it... the file size was too large..., the picture was too big... eitherway.. i finally got it done...