A Cylinder Rolling Down a Vertical Wall

[Puky]

Hello, this is not really a homework question, but a question on a specific problem so I thought it belonged here rather than the General Physics subforum. This is a problem that was asked in our final exam, and I have doubts about it's "correct" solution. Here's a paint art to explain the problem.

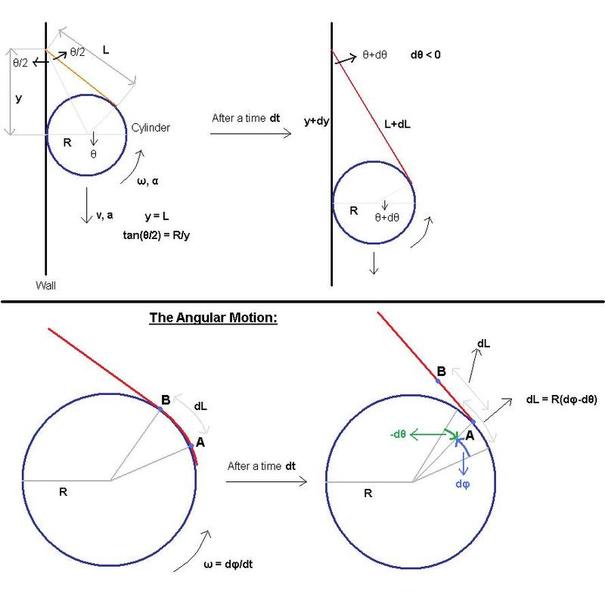
Here, a cylinder with a cord wrapped around it with one end fixed to the wall is released from rest, and it slides down as the cord unrolls. I have shown some variables on the diagram.

The question was to calculate the linear acceleration of the center of mass and the angular acceleration of the cylinder, given the needed constants like the radius and the coefficient of kinetic friction (it was small enough so that the cylinder could slide down). At the end it comes down to whether or not the magnitude of the linear acceleration a is equal to the angular acceleration \alpha times the radius R (or a = \alpha R).

Apparently, we were supposed to assume that this equation does hold, because the cord around the cylinder unrolls without slipping. It wasn't that easy to believe for me, because the direction in which the cord extends is not the same as the direction of the linear acceleration. So I did some calculation and found that the magnitude of the linear velocity v is greater than angular speed times the radius (\omega R), so a = \alpha R cannot be true. But I need to be sure if my calculation was correct.

Here is what I did:

In the diagram on the upper left, it can be seen that \tan(\frac{\theta}{2})=\frac{R}{y}.
Also, we have y=L.

Now after a time dt, the angle \theta will decrease, so d\theta is negative.

Differentiating the equation \tan(\frac{\theta}{2}) = \frac{R}{y} gives \frac{d\theta}{2\cos^2(\frac{\theta}{2})} = \frac{-R}{y^2}dy rewriting 2\cos^2(\frac{\theta}{2}) as 1+\cos(\theta) and rearranging d\theta=\frac{-R(1+\cos(\theta))}{y^2}dy.Now let's consider only the rotational motion, with the diagrams shown in the lower part of the image. Pick two points A and B on the cord such that the cord will be tangent to the cylinder at B, and the length of the cord between these points will be dL (or dy, since they are equal).

A time dt after that picture, the cord will have extended by a length dL, so the cord will be tangent to the cylinder at A, but at a different angle \theta. As shown in the image, the cylinder will rotate by an angle d\phi, and \theta will decrease by -d\theta. So these two differential angles added up will be equal to the angle between the two line segments connecting the center to A and B in the previous frame. So, dL=R(d\phi-d\theta).

Plugging in the relationship between d\theta and dy, using dL=dy and rearranging gives:(1-\frac{R^2(1+\cos(\theta))}{y^2})dy = R d\phi dividing by dt: (1-\frac{R^2(1+\cos(\theta))}{y^2})v = \omega R.

According to this, v is not equal to \omega R, but greater; and differentiating this last equation with respect to time doesn't give a=\alpha R.Thank you if you have bothered to read this far. Do you think everything I've done is correct? If anyone spots a mistake or can confirm that this is correct, I'd be glad if you could leave a reply. Thanks.

 

[TSny]

Hello, Puky.

Your work looks very good to me. That's an interesting calculation.

 

[Puky]

Hello, Puky.

Your work looks very good to me. That's an interesting calculation.

Thank you very much for going through all that. I tried explaining my work to an instructor, he wouldn't even listen, saying the differential angles d\theta and d\phi would correspond to the same angle and it was wrong to define two separate angles there.

 

[TSny]

I don’t agree with your instructor. I’m pretty sure you’re correct. As a check, I got the same result a little differently. See the attached figure. Imagine starting the cylinder with the string unwrapped a distance R so the string is horizontal. That’s the upper left position in my figure.

Next unwrap the string by moving the cylinder horizontally until the length of the string is $L = R + R\psi = R(1+\psi)$ where $\psi$ is the angle the cylinder rotates counterclockwise in unwrapping the string.

Now swing the whole thing down until the cylinder is against the wall without changing the length of the string. Then the cylinder must rotate clockwise by $\pi/2 - \theta$ where $\theta$ is the angle the string ends up making with the wall.

The net angle of rotation of the cylinder is $\phi = \psi – (\pi/2-\theta)$ so $\psi = \phi - \theta\ + \pi /2$. Then we end up with $y = L = R(1+\phi-\theta+\pi/2)$.

Using $tan(\theta/2) = \frac{R}{y}$, we have $\theta = 2*arctan(R/y)$. Hence $y = R(1+\phi-2*arctan(R/y) +\pi/2)$

Then taking the time derivative and noting $\dot{\phi} = \omega$, we get

$\dot{y} = R[\omega+2*R\dot{y}/(y^2+R^2)]$. Rearranging and letting $v = \dot{y}$ yields

$v(\frac{y^2-R^2}{y^2+R^2}) = \omega R$ which is equivalent to your result.

Only for $y>>R$ do you get $v\approx \omega R$

 

[TSny]

Sorry, the figure didn't get attached.

 

[haruspex]

Maybe this argument is short enough that your instructor will listen: consider starting with the string horizontal. At first, the angular acceleration is fairly obviously 0, but the linear acceleration is clearly > 0.

 

[Puky]

I don’t agree with your instructor. I’m pretty sure you’re correct. As a check, I got the same result a little differently. See the attached figure. Imagine starting the cylinder with the string unwrapped a distance R so the string is horizontal. That’s the upper left position in my figure.

Next unwrap the string by moving the cylinder horizontally until the length of the string is $L = R + R\psi = R(1+\psi)$ where $\psi$ is the angle the cylinder rotates counterclockwise in unwrapping the string.

Now swing the whole thing down until the cylinder is against the wall without changing the length of the string. Then the cylinder must rotate clockwise by $\pi/2 - \theta$ where $\theta$ is the angle the string ends up making with the wall.

The net angle of rotation of the cylinder is $\phi = \psi – (\pi/2-\theta)$ so $\psi = \phi - \theta\ + \pi /2$. Then we end up with $y = L = R(1+\phi-\theta+\pi/2)$.

Using $tan(\theta/2) = \frac{R}{y}$, we have $\theta = 2*arctan(R/y)$. Hence $y = R(1+\phi-2*arctan(R/y) +\pi/2)$

Then taking the time derivative and noting $\dot{\phi} = \omega$, we get

$\dot{y} = R[\omega+2*R\dot{y}/(y^2+R^2)]$. Rearranging and letting $v = \dot{y}$ yields

$v(\frac{y^2-R^2}{y^2+R^2}) = \omega R$ which is equivalent to your result.

Only for $y>>R$ do you get $v\approx \omega R$

That's a great solution! It's really smart, and much easier to visualize than than my solution. I had actually thought about doing the same thing before I came up with a different way, since moving the cylinder horizontally first makes it much easier to keep track of what is going on, but I guess I never really went about it because it doesn't exactly capture the actual rolling/sliding motion. But at the and the cylinder has done the same amount of rotation and translation because of the string, so it has to give the same answer, and does so in a more intuitive way. Thank you very much, that was really helpful.

 

[Puky]

Maybe this argument is short enough that your instructor will listen: consider starting with the string horizontal. At first, the angular acceleration is fairly obviously 0, but the linear acceleration is clearly > 0.

That was actually the first thing I tried, and apparently it wasn't obvious enough haha.

 

[TSny]

Maybe this argument is short enough that your instructor will listen: consider starting with the string horizontal. At first, the angular acceleration is fairly obviously 0, but the linear acceleration is clearly > 0.

Ah, good. In the horizontal position the tension in the string is zero and there is no net torque about the center of mass. Hence no angular acceleration at that instant. Nice to see that agrees with the equations.

 

[Puky]

I've just realized that the factor \frac{y^2-R^2}{y^2+R^2} (or that more complicated factor I found for the relationship between \omega R and v) is just equal to \cos\theta. So \omega R = v\cos\theta. This really simplifies it and it intuitively makes sense that \omega R is just equal to the component of v along the direction of the string.

 

[TSny]

I've just realized that the factor \frac{y^2-R^2}{y^2+R^2} (or that more complicated factor I found for the relationship between \omega R and v) is just equal to \cos\theta. So \omega R = v\cos\theta. This really simplifies it and it intuitively makes sense that \omega R is just equal to the component of v along the direction of the string.

Well I'll be. Super!