Finding Constants: Potential and Field Analysis

[ermia]

Homework Statement

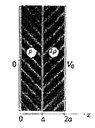
Two infinite conducting plane are a distance 2a away and parrarel. We have constant potentials on the planes. In $0<x<a$ we have charge with density $\rho$ and in $a<x<2a$ with density $2\rho$. We want to findelectric feild and potential everywhere. And to find the charge density in boundaries.

Relevant Equations

$$\nabla .E=\frac{ \rho}{\epsilon }$$
$$ E=- \nabla V$$
$$Eup -Edown = \sigma / \epsilon$$

I have wrote all feilds and potentials and I want to find the constants.
My first question is " when we say in the a<x<2a the potential is V(x)" then the potential in the a is V(a) or V(0) ( cause it is 0 in our new area) ?
Second one is " when I want to write the gausses law for the point x=a I find two feilds. Does that mean I have another surface charge in x=a?"

 

[haruspex]

Potentials are relative to some arbitrary zero. A common convention is to take it as zero at infinity, but that doesn’t work when you an infinite sheet of charge that isn't tending to zero at infinity. Take the potential as zero at x=0.
The potential at any other point can then be found by integrating the field from x=0 to the point. Note that it is necessarily continuous.

There is no surface charge at x=a in the problem.

 

[ermia]

Once I wrote gausses law for the left and write part seperately. I found two different feilds in x=a.
One is $\frac{ \rho a} {\epsilon }$ the other is $\frac{2 \rho a}{ \epsilon }$ thus we can conclude that we have a surface charge in x=a. Where am I wrong?

 

[kuruman]

Once I wrote gausses law for the left and write part seperately. I found two different feilds in x=a.
One is $\frac{ \rho a} {\epsilon }$ the other is $\frac{2 \rho a}{ \epsilon }$ thus we can conclude that we have a surface charge in x=a. Where am I wrong?

You can be wrong in many places. Most likely, you applied Gauss's law incorrectly. Please post your solution showing a clear picture (a) of the Gaussian surfaces that you used and (b) the equations that you wrote based on Gauss's law. Then we can perhaps figure out where you went wrong. We cannot reverse engineer your mistake from your answers.

 

[haruspex]

Once I wrote gausses law for the left and write part seperately. I found two different feilds in x=a.

Your attachment is illegible. If you want anyone to check your actual working you will need to type it in, per forum rules. Preferably in LaTeX.
The field at any point is due to all the charges present. Find the field due to the charges in (0,a), the field due to the charges in (a,2a), and add them together.

 

[ermia]

Your attachment is illegible. If you want anyone to check your actual working you will need to type it in, per forum rules. Preferably in LaTeX.
The field at any point is due to all the charges present. Find the field due to the charges in (0,a), the field due to the charges in (a,2a), and add them together.

Thanks. Is my answer right?
$$ \sigma_{left }= 5 \rho a $$
$$ \sigma_{right} = 6 \rho a $$