A not-so-standard buckling problem

[irishmts]

Hey guys, this came up in one of my past papers, and I'm not quite sure where to go with it.

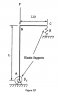
The diagram shows an idealized structure consisting of an L-shaped rigid bar structure supported b linearly elastic springs at A and C. Rotational Stiffness is denoted β_R and translational stiffness is denoted β. If β_R = 3βL²/2, determine the critical buckling load P_CR for the structure



P_CR = C²EI/L, where C is a constant which depends on the end characteristics of the bar, E is youngs modulus, I is inertia, and L is the length of the bar.

Given that the Bar is simply supported, that meant that L^e was equal to L/2 i though, and by L_e = L/sqrt(C), that gave C a value of 1/4



My first though was to try and resolve the forces being applied, so I took moments about the point of maximum deflection, L/2, when a force of P is applied, where P<P_CR. But I got lost there, because I can't figure out what the moment due to the stiffnesses would be, since they are a ratio due to the force applied/ deflection, and I don't know what deflection there would be at the point the spring is attached to

 

[Nate810]

the wall.To solve this problem, you will need to use the Euler-Bernoulli beam equation. The equation can be written as PCR = (π2EI)/L2. Since the rotational stiffness is given, you can calculate the value of I by using βR = 3βL2/2. Substituting I into the equation, you can then calculate the value of PCR.