A quarterback throws a football to a stationary receiver

  • Thread starter Thread starter Etheryte
  • Start date Start date
  • Tags Tags
    Receiver
AI Thread Summary
The discussion focuses on calculating the initial speed required for a quarterback to throw a football to a stationary receiver 31.5 meters away at a 40° angle. Participants emphasize the need to analyze the problem using two-dimensional motion equations, separating horizontal and vertical components. The initial velocity and time are the key unknowns that need to be determined through these equations. There is confusion regarding how to set the equations equal to each other due to the independent nature of the x and y components. Clear guidance is requested on formulating the equations for both motions to solve for the initial velocity and the ball's highest point.
Etheryte
Messages
3
Reaction score
0
1. Homework Statement
A quarterback throws a football to a stationary receiver 31.5m away from him. If the football is thrown at an initial angle of 40° to the ground, at what initial speed must the quarterback throw the ball for it to reach the receiver? What's the balls highest point during flight?

2. Homework Equations
ImageUploadedByPhysics Forums1429555553.253050.jpg


3. The Attempt at a Solution
ImageUploadedByPhysics Forums1429555747.953364.jpg


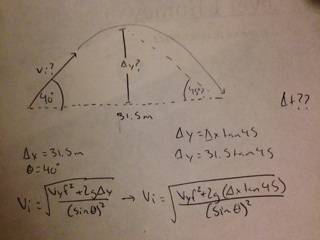
I know this is only one small attempt at rearranging the formula, but trust me if you checked my trash you'd find crumpled up pieces of paper with many more attempts.

I always go through the same procedure;
1. I make my goal to find the initial velocity.
2. To find initial velocity, I need time.
3. To find time, I need /\y.
4. To find /\y, I need the initial velocity.

Please help.
 
Physics news on Phys.org
The motion has two dimensions: vertical and horizontal. Write the equations of motion w.r.t. time for both motions. The time that the football takes to reach its destination must be the same for both horizontal and vertical motions...
 
I'm sorry, but could you please explain more in depth? I know there's two dimensions but set what two motions with which equations?
 
Etheryte said:
I'm sorry, but could you please explain more in depth? I know there's two dimensions but set what two motions with which equations?
The horizontal motion and the vertical motion. What are the equations for each?
 
Oh, the /\y and /\x equations? I thought you referred to the x and y components of the velocity..

Well, after trying to set them equal to each other — it gets to a point where the /\t can't be really set equal to the rest of the /\y equation and you have a quadratic of a sort:
ImageUploadedByPhysics Forums1429560546.830396.jpg
 
The x and y components of the trajectory are independent equations in terms of time. Write them separately to begin with. (And it would be better if you would type them in rather than attaching image. Use icons in the editing window's top bar to make subscripts or superscripts: x2, x2. Other symbols and special characters can be found using the Sigma icon).

You should then have a pair of equations that describe the motion with respect to time. The only unknowns will be the initial velocity and time. Two equations in two unknowns.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Projectile Motion of football receiver
Replies
9
Views
4K
How Should a Quarterback Throw to Hit a Stationary Receiver?
Replies
3
Views
4K
Projectile Motion - Finding Ini. Vel. using Range and Angle
Replies
3
Views
5K
Projectile Motion - What angle should the quarterback throw the football?
Replies
4
Views
6K
Catching Football (Projectile Motion)
Replies
6
Views
5K
Calculating Initial Velocity of a Football Using Projectile Motion Equations
Replies
23
Views
3K
Quadratic functions: [Diagram Included] Football game scenario
Replies
3
Views
2K
Projectile Motion Quarterback Throw
Replies
1
Views
3K
What Was the Velocity of the Football Thrown by the Quarterback?
Replies
2
Views
2K
Projectile Motion football pass
Replies
3
Views
3K

Hot Threads

Recent Insights

Back
Top