thee
- 5
- 0
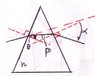
A shaft of light passes through a prism with refracting angle \theta and refractive index n. Let \alpha be the deviation angle of the shaft. Demonstrate that if the shaft of light passes through the prism symetrically the angle \alpha is the least?