badluckmath
- 9
- 3
- Homework Statement
- Show that ## \omega = \frac{\sqrt{a^{2}+g^{2} }}{l} ## for small angles
- Relevant Equations
- After solving the Hamilton equations, we find that ## \frac{d^{2}\theta}{dt^{2}} = -gsin(\theta)/l- acos(\theta)/l ##
Here is an image of the problem:
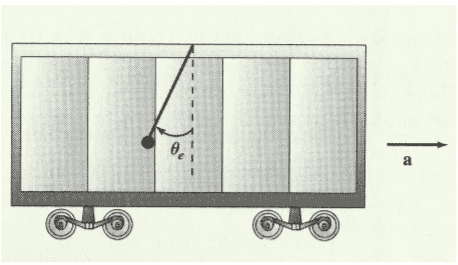 The problem consist in finding the moviment equation for the pendulum using Lagrangian and Hamiltonian equations.
The problem consist in finding the moviment equation for the pendulum using Lagrangian and Hamiltonian equations.
I managed to get the equations , which are shown insed the blue box:
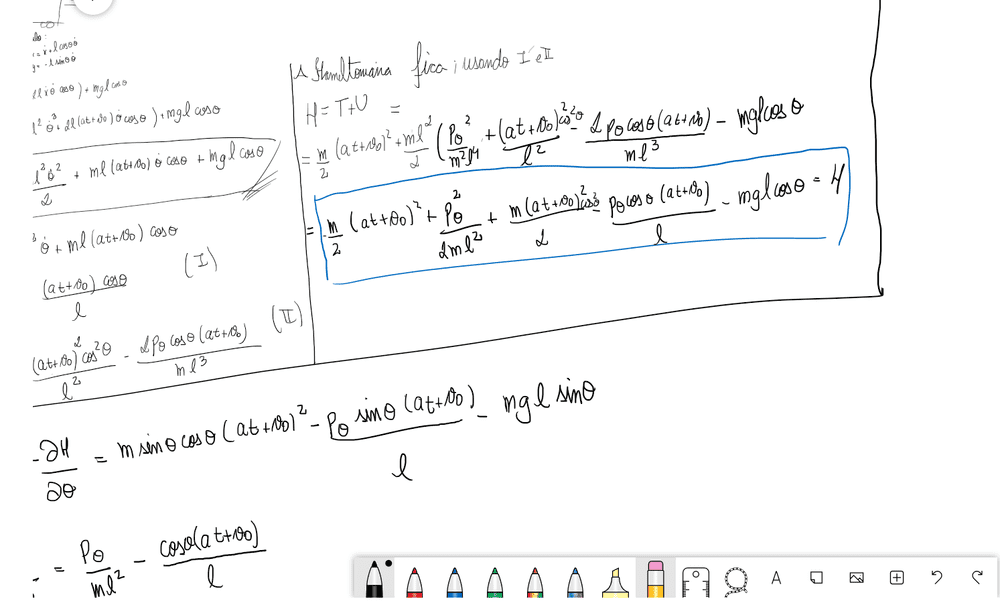
Using the hamilton equations, i finally got that the equilibrium angle ##\theta_{e}## : $$\theta_{e} = \tan^{-1}(\frac{-a}{g})$$m which is the angle where ## \frac{d^{2}\theta}{dt^{2}} =0 ##.
Now, i got stuck. I tried to solve an EDO using the small angles aproximation, but it doesn't seems to lead me anywhere, because i don't really have information for the initial values.
I managed to get the equations , which are shown insed the blue box:
Using the hamilton equations, i finally got that the equilibrium angle ##\theta_{e}## : $$\theta_{e} = \tan^{-1}(\frac{-a}{g})$$m which is the angle where ## \frac{d^{2}\theta}{dt^{2}} =0 ##.
Now, i got stuck. I tried to solve an EDO using the small angles aproximation, but it doesn't seems to lead me anywhere, because i don't really have information for the initial values.
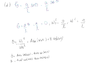

 )
)