HappyFlower
- 30
- 1
Homework Statement
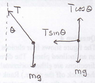
a small mass m hangs from a thing string can swing like a pendulum. You attach it above the window of your car as shown in the figure. When the car is at rest the string hangs vertically. What angle does the string make? a) when the car accelerates 1.20m/s^2 b)when the car moves at a constant velocity v=90 km/h?
Homework Equations
The Attempt at a Solution
I don't understand why the components are the way they are in the force diagram.