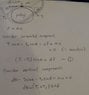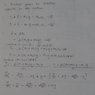A very difficult question about a pulley system with friction

[athrun200]

Homework Statement

See the picture

Homework Equations

The Attempt at a Solution

This is a very difficult, can anyone guide me step by step to finish this question.

First, let start with part(a)

In order to find the ratio, it seems we need to have the motion equations first.
I get 2 motion equations.
But I have 2 question now.
(1) Are the equation I obtained correct and useful?
(2)If it is what can I do next?(In my opinion, it would be integration, but I wonder what are the intervals.)

 

[Spinnor]

I'm a little confused, is the second jpg. the problem? If so why do you have theta in your try at the solution?

 

[athrun200]

I'm a little confused, is the second jpg. the problem? If so why do you have theta in your try at the solution?

It is because I don't know how to do
I thought that theta will be eliminated finally.

So do you have any ideas?

 

[athrun200]

Also, the answer is shocking.
It is \frac{T_{1}}{T_{2}}=e^{\mu\pi}

That why I have no idea

 

[Spinnor]

I'm a little confused, is the second jpg. the problem? ...

Maybe the original poster knows?

 

[PAllen]

I assume the second jpg is the problem and the first is the attempt at solution. The angles were introduced by the OP and are irrelevant.

One key point: there is nothing in the problem jpg about the disk rotating - only sliding is going on here.

Think about friction and gravity. Maybe start by assuming the disk is frictionless.

Show us where this takes you.

 

[athrun200]

The second picture is the question.
The first picture is my attempt to solve it.


Now if we assume the pulley is frictionless, it means we can omit it and focus on the two masses.

I obatin the following equations (see attachment).
Do these equation useful?

 

[athrun200]

Maybe the original poster knows?

He gave me another tips.
This question required integration.

 

[PAllen]

The second picture is the question.
The first picture is my attempt to solve it.


Now if we assume the pulley is frictionless, it means we can omit it and focus on the two masses.

I obatin the following equations (see attachment).
Do these equation useful?

Close so far, but you have: force - force = acceleration
in your equations. Fix this, and you'll have the frictionless case down.

Then, consider that you just 'know' the acceleration resulting from mass difference and friction. It should then be simple to extend your frictionless case to be expressed using this 'given' acceleration.

Even if integration is desired for the ultimate answer in terms of friction coefficient based on the surface properties of the string and disk, you can first consider a coefficient for the string suspended over the disk as a complete system. This has some total coefficient of friction. If you double the masses, what do you expect will happen to the total friction? So then you can easily use the prior to answer all questions in terms of a 'total system friction coefficient'.

Finally, the only step needing integration is expressing this total system coefficient in terms of standard coefficient that simply relates normal force to friction per unit length of string. On this, you need to figure the normal force between the string and disk at each point. Once you get here, I cannot help you. It has been too many years for me - I would have to review to figure out that force distribution, and I'm not inclined to do that.

 

[athrun200]

I have corrected the F=ma error and I have reached this step.

If you double the masses, what do you expect will happen to the total friction?

It will increase.

Do you mean in the integral, we have mass element dm and friction element df?

 

[PAllen]

I have corrected the F=ma error and I have reached this step.


It will increase.

Do you mean in the integral, we have mass element dm and friction element df?

Well, you can say more than 'it will increase'. If at every point, friction is proportional to normal force, and all forces in the system are doubled, then, without further ado, you can say what about the total friction?

Now, I would normally stop here, and assume you measure the system friction coefficient. But if you are required to calculate it, you need to figure out how the normal force is distributed along the disk. The integral should be just d theta, over pi radians. But what you integrate is normal force as f(theta), and friction coefficient, which is constant. It is f(theta) that I can't see offhand how to derive.

 

[athrun200]

If at every point, friction is proportional to normal force, and all forces in the system are doubled, then, without further ado, you can say what about the total friction?

Total friction also double?

Now, I would normally stop here, and assume you measure the system friction coefficient. But if you are required to calculate it, you need to figure out how the normal force is distributed along the disk. The integral should be just d theta, over pi radians. But what you integrate is normal force as f(theta), and friction coefficient, which is constant. It is f(theta) that I can't see offhand how to derive.

That means you also have no idea about how to get the answer?
My professor said he will give us the answer one month later because this is a very difficult and interesting question.

 

[PAllen]

Total friction also double?

yes

That means you also have no idea about how to get the answer?
My professor said he will give us the answer one month later because this is a very difficult and interesting question.

Correct, I can't help further without spending more time than I can afford on this. Hopefully someone else can.

NOTE: You have a few mistakes in your last set of equations.

hint 1: Your equations for tension should not include friction. That's built into m1*a or m2*a. The result will be much simpler.

hint 2: Acceleration (there is only one acceleration, as you've noted) can be obtained by noting that the sum of the net forces on each weight (involving acceleration) must equal the balance of gravitation forces and friction.

The overall results should be quite simple (at least in terms of total system coefficient of friction).

 

[NascentOxygen]

One key point: there is nothing in the problem jpg about the disk rotating

True. But it seems to be drawn to resemble a pulley, and we are told to consider the disc to be massless...

- only sliding is going on here.

Maybe.

OP: Did you originate the word "pulley" in the subject line, or was it in the heading of the questions where you sourced this?

 

[athrun200]

OP: Did you originate the word "pulley" in the subject line, or was it in the heading of the questions where you sourced this?

Sorry, I don't understand what you mean. Are you asking where did I get this question?

 

[NascentOxygen]

Was this in a chapter titled Motion and Pulleys? Or did you think it looked like a pulley so put that in your subject header, though the chapter didn't mention pulleys?

 

[athrun200]

Was this in a chapter titled Motion and Pulleys? Or did you think it looked like a pulley so put that in your subject header, though the chapter didn't mention pulleys?

My professor just gave this question to us during the tutorial class. All the question are related to writing equations.

I don't know if he extract it from the chapter of pulley. (We haven't leart pulley yet)

 

[PAllen]

True. But it seems to be drawn to resemble a pulley, and we are told to consider the disc to be massless...


Maybe.

OP: Did you originate the word "pulley" in the subject line, or was it in the heading of the questions where you sourced this?

I did notice that wording. But then, either:

1) masslessness is irrelevant, but friction is important and the problem is fully specified (and lives up to being hard if you are to integrate from a simple coefficient of friction).
or
2) if pulley is assumed (and assumed to have no rolling friction), then masslessness is relevant but friction is irrelevant and problem is completely trivial.
or
3) if both rolling and sliding are going on, the problem is underspecified and unsolvable.

It seems to me (1) is the only assumption that makes the problem both interesting and solvable.

 

[NascentOxygen]

It seems to me (1) is the only assumption that makes the problem both interesting and solvable.

There's a red herring somewhere. But the fact that athrun200 says the supplied answer involves e^{(coeff frict)} points to this not being a pulley. A fixed shaft then.

So, athrun200, can you do integral calculus?

 

[athrun200]

There's a red herring somewhere. But the fact that athrun200 says the supplied answer involves e^{(coeff frict)} points to this not being a pulley. A fixed shaft then.

So, athrun200, can you do integral calculus?

Yes, I am taking a course about multivariable calculus and it covers integral calculus.
Does this question requires it?

 

[NascentOxygen]

Yes, this is a problem in calculus. I can see how to go about it, but doubt that I can complete it. I'll give it more thought tomorrow, if no one has come to the rescue.

Unless you have been given a worked example of this, I doubt that you would be expected to see how to do it from scratch. It looks like involving integration in polar coordinates.

Do you work co-operatively with other students? Two heads are better than one. I'm thinking that another student might tell you to just copy a worked example from your lecture notes, but change the data values!

 

[athrun200]

Do you work co-operatively with other students? Two heads are better than one. I'm thinking that another student might tell you to just copy a worked example from your lecture notes, but change the data values!

I tried to invite them to think about it together, but they said that this is not related to the exam and are not interested in this.
My professor said this question is just for fun.

 

[PAllen]

I hope I have guided athrun200 to a complete solution in terms of 'total system coefficient of friction'. That part is simple. Then you need integration to derive this from regular coefficient of friction based on the distribution of normal force around the upper half of the disk. You then just plug this integrated value into the solution I have guided you to.

Unfortunately, the integration part is what neither me nor NascentOxygen are jumping to do. For me, I think I would need to research a little how the normal force would be distributed. I can't come up (so far) with a convincing argument for the nature of this distribution.

 

[athrun200]

I think I might do it few days later since I need to finish my homework and prepare for the test.