esmeco
- 144
- 0
Homework Statement
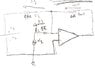
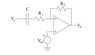
The problem states that we should draw the Vout curve of an amplifier circuit.
Homework Equations
We have a sinusoidal sign with amplitude=1v and frequency=0.5
v(t)=A*sin(2pi*f*t)
f=1/T
T=2s
The Attempt at a Solution
Since we have negative feedback: Vp=Vn
The currents for this circuit would be:
I1+I2=Iout
I1=(0-1)/0.5=-2
I2=(0-v1)/1=-v1
Iout=(Vout-0)/2
I know that:
V1=1*sin(2pi*0.5*2)=0
So,the final equation would be: Vout=(-1*2)/0.5=-4v
Does this look ok?Also,when drawing the curve for vout,vout is the amplitude of the curve right?Or is the amplitude of the curve related to vout 1volt?