- #1
Martin Harris
- 103
- 6
- Homework Statement
- AC Circuit Phasors
- Relevant Equations
- Kirchoff's and Ohm's Law
Summary:: Hi, I tried attempting this problem in alternating current in order to find out the phasors as complex numbers, and I would be more than grateful if someone could peer review it, and confirm my calculations (Please see below both the Figure and the calculations)
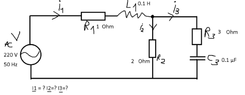
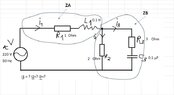
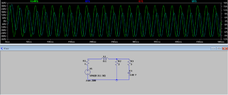
Please find attached the electrical circuit as a figure.
Given data:
I1, I2, I3 =? (Phasors as complex numbers for alternating current)
From Ohm's Law:
$$I = \frac V Z (Eq1)$$where I = current, V= Voltage and Z = impedance
From Kirchoff's Law:
$$I=I1=I2+I3 (Eq2)$$
Given that branches containing R2 and R3 with C3 are in | | (parallel), then:
$$V2=V3$$
and
$$\frac{1}{Z}= \frac{1}{Z_1}+\frac{1}{Z_2} (Eq3)$$
$$Z_1=R1+iωL = R1 + i*2π*F*L (Ω)$$ where i is the imaginary part of the impedance
$$Z_1=1Ω + (2*π* 50Hz *0.1H* i) Ω $$
$$ Z1 = (1+31.41592 i)Ω $$
$$Z2=R2=2Ω$$
(Z2 just 2Ω since it's just the resistance, it won't appear as a complex number impedance)
$$Z3 = R3-ixC3 = 3 Ω-\frac{1}{2*π*F*C} = 3 Ω-\frac{1}{2*π*50Hz*10^-7 F}i Ω $$
$$Z3 = (3 - 31830.988i) Ω$$
From Eq3:
$$\frac{1}{Z}= \frac{1}{(1+31.41592 i)Ω}+\frac{1}{2Ω} $$
According to Microsoft MathSovler
$$Z=(1.987950624+0.126177045i) Ω $$
$$From Eq1: I1 = I = \frac V Z $$
$$I= \frac {220V} {(1.987950624+0.126177045i)Ω} $$
$$I1= (110.276245603−6.992857044i)A $$
$$ From Eq2 (Kirchoff's Law): I2=I1-I3 = (110.276245603−6.992857044i)A - I3 (Eq4) $$
$$ V2=V3$$ hence $$I2*Z2=I3*Z3 (Eq5)$$
Substituting Eq4 into Eq5 yields:
$$(110.276245603−6.992857044i)A * 2Ω = I3 * (3 - 31830.988i) Ω$$
Solving for I3 (According to Microsoft Math Solver)
$$I3 = (0.000440024+0.006928817i) A $$
Now from Eq5 we can solve for I2 =I1-I3
$$I2=(110.276245603−6.992857044i)A - (0.000440024+0.006928817i) A$$
$$I2 = (110.27576−6.999728 i)A$$
I am really confused why I3 is so low though, for sure I did something wrong because I3 has negative value both on the real and imaginary part.
I would be more than grateful if someone could check my work as a peer review.
Please find attached the electrical circuit as a figure.
Given data:
| Voltage V | 220 V |
| Frequency | 50 Hz |
| Resistance R1 | 1 Ω |
| Coil electrical inductance L1 | 0.1 H |
| Resistance R2 | 2 Ω |
| Resistance R3 | 3 Ω |
| Capacitor electrical capacitance C3 | 0.1 μF = 10-7 F |
From Ohm's Law:
$$I = \frac V Z (Eq1)$$where I = current, V= Voltage and Z = impedance
From Kirchoff's Law:
$$I=I1=I2+I3 (Eq2)$$
Given that branches containing R2 and R3 with C3 are in | | (parallel), then:
$$V2=V3$$
and
$$\frac{1}{Z}= \frac{1}{Z_1}+\frac{1}{Z_2} (Eq3)$$
$$Z_1=R1+iωL = R1 + i*2π*F*L (Ω)$$ where i is the imaginary part of the impedance
$$Z_1=1Ω + (2*π* 50Hz *0.1H* i) Ω $$
$$ Z1 = (1+31.41592 i)Ω $$
$$Z2=R2=2Ω$$
(Z2 just 2Ω since it's just the resistance, it won't appear as a complex number impedance)
$$Z3 = R3-ixC3 = 3 Ω-\frac{1}{2*π*F*C} = 3 Ω-\frac{1}{2*π*50Hz*10^-7 F}i Ω $$
$$Z3 = (3 - 31830.988i) Ω$$
From Eq3:
$$\frac{1}{Z}= \frac{1}{(1+31.41592 i)Ω}+\frac{1}{2Ω} $$
According to Microsoft MathSovler
$$Z=(1.987950624+0.126177045i) Ω $$
$$From Eq1: I1 = I = \frac V Z $$
$$I= \frac {220V} {(1.987950624+0.126177045i)Ω} $$
$$I1= (110.276245603−6.992857044i)A $$
$$ From Eq2 (Kirchoff's Law): I2=I1-I3 = (110.276245603−6.992857044i)A - I3 (Eq4) $$
$$ V2=V3$$ hence $$I2*Z2=I3*Z3 (Eq5)$$
Substituting Eq4 into Eq5 yields:
$$(110.276245603−6.992857044i)A * 2Ω = I3 * (3 - 31830.988i) Ω$$
Solving for I3 (According to Microsoft Math Solver)
$$I3 = (0.000440024+0.006928817i) A $$
Now from Eq5 we can solve for I2 =I1-I3
$$I2=(110.276245603−6.992857044i)A - (0.000440024+0.006928817i) A$$
$$I2 = (110.27576−6.999728 i)A$$
I am really confused why I3 is so low though, for sure I did something wrong because I3 has negative value both on the real and imaginary part.
I would be more than grateful if someone could check my work as a peer review.
Attachments
Last edited: