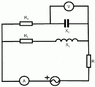
- #1
R A V E N
- 64
- 0
Homework Statement
In circuit given in attachment,find the value which is showed on ammeter A,if voltmeter is showing [tex]50\;V[/tex].
Values are [tex]R=R_2=X_L=X_C=10\;\Omega[/tex] and [tex]R_1=5\;\Omega[/tex].
The Attempt at a Solution
First I calculate current thought branch with [tex]R_2[/tex] and [tex]X_C[/tex]:
[tex]\underline{I}_2=\frac{\underline{U}}{-jX_C}=j5\;A[/tex]
then knowing that potential difference at the ends of branches(one with [tex]R_2[/tex] and
[tex]X_C[/tex] and the other with [tex]R_1[/tex] and [tex]X_L[/tex]) is the same,I proceed:
[tex]\underline{U}_1=\underline{U}_2[/tex]
[tex]\frac{\underline{I}_1}{R_1+jX_L}=\frac{\underline{I}_2}{R_2-jX_C}[/tex]
[tex]\underline{I}_1=\frac{R_1+jX_L}{R_2-jX_C}\underline{I}_2=(-3.75-j1.25)\;A[/tex]
Overall current [tex]\underline{I}[/tex] in circuit is the sum of two currents from two branches,so:
[tex]\underline{I}=\underline{I_1}+\underline{I_2}=(-3.75+j3.75)\;A[/tex]
Module of this value is value showed on ammeter:
[tex]|\underline{I}|=5.303\;A[/tex]
However,correct solution is:
[tex]3\sqrt{5}\;A\approx6.708\;A[/tex]
Where is the mistake?
Attachments
Last edited: