Accelerating Ions through semicircular plates

[tmvphil]

Homework Statement

Hey guys, this is from Purcell 3.19
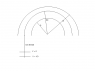
"Ions are accelerated through a potential difference V_0 and then enter the space between the semicylindrical electrodes A and B. Show that an ion will follow the semicircular path of radius r_0 if the potentials of the outer and inner electrodes are maintained, respectively, at 2V_0*ln(b/r_0) and 2V_0*ln(a/r_0)."

Homework Equations

The Attempt at a Solution

Well i started with
q*V_0 = KE = (mv^2)/2
so
V^2 = (2qV_0)/m
which combined with the rotational motion eq
E = F/q = (mv^2)/(qr_0) = (2V_0)/r_0
but i can't think of any way to pin down what the field is between the two cylinders.
just looking at the solution provided it seems like i should integrate the final equation for a variable r from b to r-nought and a to r-nought. I just don't know why. Any way to elucidate this for me?

 

[tmvphil]

Attached a diagram (sorry for the paint) if it helps make it clearer