TimelessTime
- 5
- 0
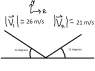
Problem: A hockey puck rebounds from a board as shown in figure 16. The puck is in contact with the board for 2.5 ms. Determine the average acceleration of the puck over the interval.
t = 0.0025 s |vi|= 26 m/s |vf| = 21 m/s aav = ? *v and a are vectors*
I have made several attempts to solve this question and have seen the previous thread about this question and I am still unable to get the correct answer. The correct answer is
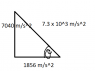
7.3 x 10^3 m/s^2[7.5 N of W]. In my opinion my closest attempt was that I broke the initial vector and final vector into components, found the change in vx to equal 4.6 m/s and the change in vy to equal -1.9 and then found the change in v to equal 5. my final answer and direction were completely wrong. Can someone help me with this awful question?
t = 0.0025 s |vi|= 26 m/s |vf| = 21 m/s aav = ? *v and a are vectors*
I have made several attempts to solve this question and have seen the previous thread about this question and I am still unable to get the correct answer. The correct answer is
7.3 x 10^3 m/s^2[7.5 N of W]. In my opinion my closest attempt was that I broke the initial vector and final vector into components, found the change in vx to equal 4.6 m/s and the change in vy to equal -1.9 and then found the change in v to equal 5. my final answer and direction were completely wrong. Can someone help me with this awful question?