pochemuchka
- 4
- 0
- Homework Statement
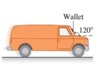
- You are driving at a reasonable constant velocity in a van with a windshield tilted 120∘ relative to the horizontal. As you pass under a utility worker fixing a power line, his wallet falls onto the windshield. Assume the coefficient of static friction between the glass and the wallet to be 0.50.
- Relevant Equations
- F=ma, N=-mg, Fg=mg, Fs=(mu)N
I think I am on the right path but I'm having trouble cancelling out the mass of the wallet. I drew a free body diagram and know that there are three forces acting on the wallet: gravity, friction, and normal force (including the van's acceleration).
The y-component of the friction and normal forces should cancel the force of gravity. I have the equation as mg = sin60(mu)(N) + sin30(N) [N is normal force].
I don't know how to cancel out the mass so I can use the normal force to find acceleration in the x-direction. Any help?
The y-component of the friction and normal forces should cancel the force of gravity. I have the equation as mg = sin60(mu)(N) + sin30(N) [N is normal force].
I don't know how to cancel out the mass so I can use the normal force to find acceleration in the x-direction. Any help?