randomgamernerd
- 139
- 4
Homework Statement
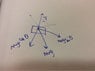
:A block B of mass m is suspended from a cord of length l attached to cart A of mass M as shown in the figure. The horizontal surface on which the cart moves is smooth. Initially the cart and the block are at rest in the position shown. Now the block is released. Take M=2kg, θ=45⁰ and g=10m/s².
Acceleration of the cart immediately after the system is released from rest and tension in the cord developed immediately is?
Homework Equations
: [/B]Balancing components of forces.The Attempt at a Solution
; [/B]so as soon as the system is released from rest, tension in the chord acts, and I think that is because of mgCosθ . So tension should be 20cos45⁰ which is not the answer.
For horizontal acceleration of cart, I’m confused. I believe tension force gives the horizontal component of force which is responsible for accelertion of the cart. But since no external force is acting on the system, then centre of mass should not move, which means it will have acceleration in opposite direction of acceleration of block B. After this i don't know what to do.
Sorry for poor quality of the image.