Acceleration of block 1 in a pulley system

[ShizukaSm]

Homework Statement

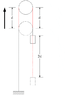
http://prntscr.com/otut8
Find acceleration of block 1, knowing that the mass of block 1 is 2kg and of block 2 is 4kg. You may ignore friction and pulley mass.

Homework Equations

Fr = ma

The Attempt at a Solution

I Drew free body diagrams to block 1, 2 and the pulley, then made the equations:
<br /> \\<br /> \sum F_{r2} = m_2a_2\\<br /> P_2 - T_2 = m_2a_2\\<br /> \\<br /> \sum F_{rpulley} = m_{pulley}*a\\<br /> 2T_2 = T_1\\<br /> \\<br /> \sum F_{1}=m_1a_1\\<br /> T_1=m_1a_1\rightarrow T_2 = \frac{m_1a_1}{2}<br /> <br /> \\\\a_1=2a_2 \rightarrow T_2=\frac{m_1(2a_2)}{2} = m_1a_2<br /> <br /> \\(Substituting\ in \ first\ equation)\\<br /> P_2-(m_1a_2)= m_2a_2\\<br /> a_2(m_2+m_1) = m_2*g\\\\<br /> a_2=\frac{m_2g}{m_2+m_1} = 6.53\frac{m}{s^2}\rightarrow a_1 = 13.06\frac{m}{s^2}<br />
The answer, however, is supposed to be 4.4 m/s²


Thanks in advance!

 

[gneill]

Is $a_1 = 2 a_2$ true?

 

[ShizukaSm]

Well, I think it is, isn't it?

If 1 moves a distance "d", 2 will move only d/2 because the rope has to run on both sides of the pulley.

 

[gneill]

Well, I think it is, isn't it?

If 1 moves a distance "d", 2 will move only d/2 because the rope has to run on both sides of the pulley.

On the other hand, if 1 moves a distance "d", the pulley "takes" a length "d" of rope from both sides of the pulley. This rope can only come from the free end holding m2.

 

[ShizukaSm]

Wow, that... that makes a lot of sense, so in fact a1 = 2a2

Thanks a lot, gneill!