Acceleration of Block B in a Constrained Motion Problem

[Saitama]

Homework Statement

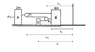
Calculate the acceleration of the block B in the figure, assuming the surfaces and the pulleys $P_1$ and $P_2$ are all smooth and pulleys and string are light.

(The mass of block C is m)

Ans: F/(7m)

Homework Equations

The Attempt at a Solution

I measured distances from a fixed wall on the right of B. The distances are shown in the second attachment.
Writing down the expression for length of string, ($R$ is the radius of pulleys)
$$L=x_{P1}-x_B+\pi R+x_{P1}-x_{P2}+\pi R+x_{C}-x_{P2}$$
Differentiating twice with respect to time,
$$0=2\ddot{x_{P1}}-\ddot{x_B}-2\ddot{x_{P2}}+\ddot{x_{C}}$$
$\because \ddot{x_{P1}}=\ddot{x_A}$ and $\ddot{x_{P2}}=\ddot{x_{B}}$
$$2\ddot{x_A}=3\ddot{x_B}-\ddot{x_C} (*)$$
Assume that the tension in the string is T. Applying Newton's second law for A,
$$F-2T=2m\ddot{x_A} (**)$$
For B,
$$3T=4m\ddot{x_B} (***)$$
For C,
$$T=m\ddot{x_C} (****)$$
Solving the four equations,
\ddot{x_B}=\frac{3F}{13m}

Any help is appreciated. Thanks!

 

[Tanya Sharma]

I would suggest to keep things simple.

Let the lengths be x1(top),x2(middle),x3(bottom).

A and B move to the left,C move to the right.

We have, \ddot{x_1}+\ddot{x_2}+\ddot{x_3}=0

\ddot{x_1}=a_A-a_B

\ddot{x_2}=a_A-a_B

\ddot{x_3}=-a_B-a_C

where a_A,a_B,a_C are magnitude of accelerations of blocks A,B,C.

a_A = (F-2T)/(2m)

a_B = 3T/(4m)

a_C= T/m

 

[Saitama]

I would suggest to keep things simple.

Let the lengths be x1(top),x2(middle),x3(bottom).

A and B move to the left,C move to the right.

We have, \ddot{x_1}+\ddot{x_2}+\ddot{x_3}=0

\ddot{x_1}=a_A-a_B

\ddot{x_2}=a_A-a_B

\ddot{x_3}=-a_B-a_C

where a_A,a_B,a_C are magnitude of accelerations of blocks A,B,C.

a_A = (F-2T)/(2m)

a_B = 3T/(4m)

a_C= T/m

That does gives the answer but how do you get the second derivatives of lengths in terms of $a_A$, $a_B$ and $a_C$?
Using your method, I get $2a_A=3a_B+a_C$ where as from my method, I get $2a_A=3a_B-a_C$. Where did I go wrong?

 

[Tanya Sharma]

That does gives the answer but how do you get the second derivatives of lengths in terms of $a_A$, $a_B$ and $a_C$?

Lets consider case of x1:

What causes a change in x1?

Block A moving to the left causes x1 to increase and B moving to the left causes the string length x1 to decrease.So, \dot{x_1}={v_A}-{v_B},where {v_A} and{v_B} are speeds of a and B respectively.

Hence \ddot{x_1}=\ddot{a_A}-\ddot{a_B}.

 

[Saitama]

Lets consider case of x1:

What causes a change in x1?

Block A moving to the left causes x1 to increase and B moving to the left causes the string length x1 to decrease.So, \dot{x_1}={v_A}-{v_B},where {v_A} and{v_B} are speeds of a and B respectively.

Hence \ddot{x_1}=a_A-a_B.

Thanks! :)

Any idea what's wrong with my method?

 

[Tanya Sharma]

For C,
$$T=m\ddot{x_C} (****)$$

It should be $$-T=m\ddot{x_C} (****)$$

You are considering left direction to be positive .

 

[Saitama]

It should be $$-T=m\ddot{x_C} (****)$$

You are considering left direction to be positive .

Great! Thanks a lot Tanya! :)