Nanoath
- 8
- 0
http://img297.imageshack.us/img297/5664/systemofobjectssq1.jpg"
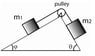
Find the acceleration of the system of two masses shown in the figure, given that m1 = 10 kg, m2 = 20 kg, θ = 60o and φ = 30o. Assume that the incline plane is smooth (i.e., there is no friction) and that g = 10 m/s2.
A: T=m_{2}g*sinθ + m_{1}g*sinφ
B: T_{1}=T_{2}
C: F=ma
T_{total}=223.2 using A
-----
F=m_{2}g*sinθ - m_{1}g*sinφ
F=123.21
-----
Using C: a=F/m
a=m_{2}g*sinθ - m_{1}g*sinφ / m_{1} + m_{2}
a= 4.11m/s^{2}
I'm not sure how to approach this one...
I know tension = T_{1}=T_{2}...
Then i get the Force that will be going right since m_{1} < m_{2}
and find the acceleration. I just want someone to see if I understood this right.
I was trying to approach the masses as two different components, but it didn't work that well..
Homework Statement
Find the acceleration of the system of two masses shown in the figure, given that m1 = 10 kg, m2 = 20 kg, θ = 60o and φ = 30o. Assume that the incline plane is smooth (i.e., there is no friction) and that g = 10 m/s2.
Homework Equations
A: T=m_{2}g*sinθ + m_{1}g*sinφ
B: T_{1}=T_{2}
C: F=ma
The Attempt at a Solution
T_{total}=223.2 using A
-----
F=m_{2}g*sinθ - m_{1}g*sinφ
F=123.21
-----
Using C: a=F/m
a=m_{2}g*sinθ - m_{1}g*sinφ / m_{1} + m_{2}
a= 4.11m/s^{2}
I'm not sure how to approach this one...
I know tension = T_{1}=T_{2}...
Then i get the Force that will be going right since m_{1} < m_{2}
and find the acceleration. I just want someone to see if I understood this right.
I was trying to approach the masses as two different components, but it didn't work that well..
Attachments
Last edited by a moderator: