Ctom101
- 3
- 0
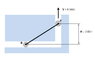
1. A link is connected by two bearings A and B. The bearings run along slots which are at right angles to each other. The length of the link AB (length between the centres of bearings A and B) is 0.2m. At an instant of time, height H, is 0.05m, and the bearing A has a constant velocity V, of 0.1m/s upwards.
At the instant of time calculate;
The velocity of bearing B.
The angular velocity of the link AB.
The acceleration of bearing B.
The angular acceleration of the link AB
2. velocity B = distance from rotational centre x angular velocity of link AB.
angular velocity of link AB = velocity A / distance from centre of zero velocity
3. from the working out in my picture changing it into a triangle I think I have worked out the velocity of bearing B and the angular velocity of link AB, but I don't know how to find the acceleration of B or the angular acceleration of AB.
Could somebody please help me with this and let me know if what I've done so far is incorrect?
a = 0.05 c = 0.2
a2 + b2 = c2
0.22 / 0.052 = 16 root 16 = 4 b = 4
velocity A / distance from centre of zero velocity
0.1 / 0.05 = 2rad/s angular velocity of link AB
velocity B = distance from rotational centre(b) x angular velocity link AB
4 x 2 = 8m/s
ωv AB = 2rad/s
v B = 8m/s
At the instant of time calculate;
The velocity of bearing B.
The angular velocity of the link AB.
The acceleration of bearing B.
The angular acceleration of the link AB
2. velocity B = distance from rotational centre x angular velocity of link AB.
angular velocity of link AB = velocity A / distance from centre of zero velocity
3. from the working out in my picture changing it into a triangle I think I have worked out the velocity of bearing B and the angular velocity of link AB, but I don't know how to find the acceleration of B or the angular acceleration of AB.
Could somebody please help me with this and let me know if what I've done so far is incorrect?
The Attempt at a Solution
a = 0.05 c = 0.2
a2 + b2 = c2
0.22 / 0.052 = 16 root 16 = 4 b = 4
velocity A / distance from centre of zero velocity
0.1 / 0.05 = 2rad/s angular velocity of link AB
velocity B = distance from rotational centre(b) x angular velocity link AB
4 x 2 = 8m/s
ωv AB = 2rad/s
v B = 8m/s
Attachments
Last edited: