Actual Depth and Apparent Depth

[chibi_lenne]

Okay, I need a bit of a jump start with this question, I know how to find the Apparent depth normally, but I've never done actual depth and I can't really figure it out (*stupid*)

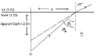
11. Frederika is sitting in her fishing boat observing a rainbow trout swimming below the surface of the water. She guesses the apparent depth of the trout at 2.0m. She estimates that her eyes are about 1.0m above the water's surface, and that the angle at which she's observing the trout is 45degrees...

b)Calculate the actual depth of the trout.

please help ~_~

 

[Dr.Brain]

Ok I hope you know something about "what refractive index" does ?

If we are looking from air into water then the refractive index m is related as:

<br /> m=\frac{realdepth}{apparentdepth}<br />

First try to draw figure of above situation using correct laws for refraction and a good ray diagram will definitely help..show your work...help will follow..

 

[Ouabache]

If your fuzzy on refraction you might want to take a look at this reference
If you read along, you will see they discuss depth perception.

I agree with Doc, to try and draw a complete diagram of the information given. It makes the analysis much easier.

 

[chibi_lenne]

I decided to give my brain a bit of a rest on this problem and moved forward. I think I may have it, I'd still like to see if it's accurate or get help if it's completely wrong (which is very likely) Here's what I have so far:
Analysis:

n = 1.33 for water
n[2]= 1.00 for air

Actual depth= (sine{angle}i)(d)

tanZ = tan{angel}R = d/h, therefore d= (h)(tan{angle}R)

{Angle}R = (n)(sin{angle}i)/(n[2])

Solution:

sin{angle}R = (3.00)(0.071)/(1.00)

= 0.9404
{angle)R = 70.1*​

d = (3.0m)(tan70.1*)
= (3.0m)(2.762)
= 8.286m

Actual Depth = (sin{angle}i)(d)

= (sin45*)(8.286m)
= (0.7071)(8.286m)
= 5.859m​

Therefore the actual depth of the fish is 5.859m.
Hope this is right this problem is driving me nuts!

 

[Doc Al]

Actual depth= (sine{angle}i)(d)

According to your diagram, that should be: Actual depth = d/ \tan \theta_i. Note that d = 2.0 m, since \theta_r is 45 degrees.

 

[chibi_lenne]

According to your diagram, that should be: Actual depth = d/ \tan \theta_i. Note that d = 2.0 m, since \theta_r is 45 degrees.

Now I'm confused...how is d = 2.0m? if I did the equation for actual depth with that as d, it would mean the actual depth is the same as the apparent depth?

Actual depth = (2.0m)/tan45*

= (2.0m)/(1.0)
= 2.0m​

 

[Doc Al]

Now I'm confused...how is d = 2.0m?

This can be deduced from the statement of the problem: The apparent depth is 2 m and the angle is 45 degrees.

if I did the equation for actual depth with that as d, it would mean the actual depth is the same as the apparent depth?

No.

Actual depth = (2.0m)/tan45*

= (2.0m)/(1.0)
= 2.0m​

No. Actual depth = d/ \tan \theta_i, not d/ \tan \theta_r

 

[chibi_lenne]

okay, so I have to find the angle of incidence...so how do I do that? x.x

 

[Doc Al]

By applying Snell's law for refraction.

 

[chibi_lenne]

duh *slaps forhead* alright I have to rearrange the formula, I feel stupid now. So it should be:

(ni)(sin{angle}i) = (nR)(sin{angle}R) so therefore

sin{angle}i = (ni)/(nR)(sin{angle}R) ?

 

[Doc Al]

I believe you made an error in reaching your second equation.

Snell's law tells us:
n_1 \sin \theta_1 = n_2 \sin \theta_2

So:
\sin \theta_1 = (n_2/n_1) \sin \theta_2

 

[chibi_lenne]

I believe you made an error in reaching your second equation.

Snell's law tells us:
n_1 \sin \theta_1 = n_2 \sin \theta_2

So:
\sin \theta_1 = (n_2/n_1) \sin \theta_2

ooo I see, (forgot to put in an extra set of () ) so it should be:

\sin \theta_i = (1.00/1.33) (0.8509)
<br /> = 0.6398
\theta_i = 39.6*


??

 

[Doc Al]

\sin \theta_i = (1.00/1.33) (0.8509)

Where does the "0.8509" come from??

 

[chibi_lenne]

Where does the "0.8509" come from??

0.8509 = \sin45*

Or at least that is what I was doing...

 

[Doc Al]

Better double check that result!

 

[chibi_lenne]

gah what am I doing wrong? x.x

 

[Doc Al]

Ah, now I see what you did... You have your calculator set for radians, not degrees.

 

[chibi_lenne]

*mutters something about incompitant calculators*

So it should be something like this?

\sin \theta_i = (n_i / n_R)\sin \theta_R
= (1.00 / 1.33 )(\sin45*)
= (0.7519)(0.7071)
= 0.5317
\theta_i = 32.1*

Actual Depth = (2.0m)/(\tan32.1*)
= (2.0m)/(0.6277)
= 3.18m

Making the actual depth of the fish 3.2m??

I hope this is it, or close anyway.

 

[Doc Al]

Looks good to me!

 

[chibi_lenne]

Yay! Thanks so much! I really appreciate the help and for you putting up with my massive brain malfunction ^_^()