Victorzaroni
- 46
- 0
Homework Statement
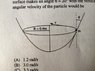
A particle of mass m rotates with a uniform speed on the inside of a bowl's parabolic frictionless surface in a horizontal circle of radius R=0.4 meters as shown below. At the position of the particle the surface makes an angle θ=20 degrees with the vertical. The angular velocity of the particle would be:
Homework Equations
?
The Attempt at a Solution
I have no idea what to do. The answer is 8.2rad/s