Poppietje
- 3
- 0
Hello!
This is probably a rather simple problem, but I've been a bit confused about how to approach it. Any kick in the right direction for problem b) would be much appreciated! (Below is the full problem statement and sub-questions also for those who want to practice their physics. The question that I need help with is in bold.)
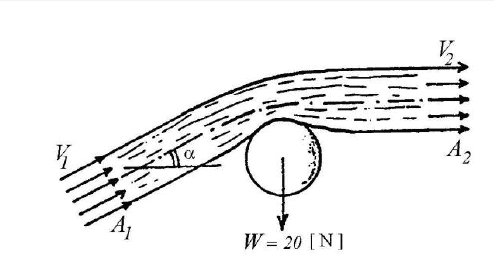
A sphere with a weight W = 20N "hangs" under a free homogeneous jet of air. The jet is deflected by the sphere, the original angle α changes to the horizontal. The velocity of the jet before deflection V1 = 20 m/s, the cross-sectional area before deflection A1 = 0.25m2. The air density ρ = 1.2 kg/m3.
Viscous forces on the sphere are neglected.
a) Choose a control volume and draw a vector diagram showing the relationship between the force on the jet and the momentum per second entering and leaving the control volume.
b) Calculate the angle α of the jet before deflection.
Calculate c) V2 and d) A2 of the jet after deflection.
At this point, all of our problems are to be solved using Bernoulli's equation, the Continuity equation and the Momentum equation. (Though I figure that the angle part is just pure trigonometry. :) )
For problem b):
My instinct would be to just take the tan-1 of the values opp./adj., as taught by trigonometry. Problem is, I have no idea how to define these values. I did calculate that the force of the flow at the inlet area is 120N assuming that the flow travels horizontally, giving us what could be used as the value for the adjacent side. I'm just not convinced of if this is the correct approach for solving for α, and even if it was, I'm not sure how to proceed with this information.
Any help would be greatly appreciated! Thank you!
This is probably a rather simple problem, but I've been a bit confused about how to approach it. Any kick in the right direction for problem b) would be much appreciated! (Below is the full problem statement and sub-questions also for those who want to practice their physics. The question that I need help with is in bold.)
Homework Statement
A sphere with a weight W = 20N "hangs" under a free homogeneous jet of air. The jet is deflected by the sphere, the original angle α changes to the horizontal. The velocity of the jet before deflection V1 = 20 m/s, the cross-sectional area before deflection A1 = 0.25m2. The air density ρ = 1.2 kg/m3.
Viscous forces on the sphere are neglected.
a) Choose a control volume and draw a vector diagram showing the relationship between the force on the jet and the momentum per second entering and leaving the control volume.
b) Calculate the angle α of the jet before deflection.
Calculate c) V2 and d) A2 of the jet after deflection.
Homework Equations
At this point, all of our problems are to be solved using Bernoulli's equation, the Continuity equation and the Momentum equation. (Though I figure that the angle part is just pure trigonometry. :) )
The Attempt at a Solution
For problem b):
My instinct would be to just take the tan-1 of the values opp./adj., as taught by trigonometry. Problem is, I have no idea how to define these values. I did calculate that the force of the flow at the inlet area is 120N assuming that the flow travels horizontally, giving us what could be used as the value for the adjacent side. I'm just not convinced of if this is the correct approach for solving for α, and even if it was, I'm not sure how to proceed with this information.
Any help would be greatly appreciated! Thank you!