- #1
ara_anandv
- 6
- 0
Hi,
Please help me in solving this problem.
I need to calculate the dia of the Allen screw.
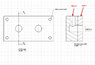
I have an assembly (2 parts).
Hydraulic fluid is passing thru the drilled hole.
I need to calculate the dia of the Allen screw (for fastening 2 plates).
The load is acting parallel to the fluids flow.
If the load is acting vertically I know the calculation to get the dia of the Allen screw.
In this case the load is parallel.
If the load is vertical the total load is divided be the number of bolts, which gives the load acting on each bolt, from that cross sectional area is calculated and from the Area dia of the bolt is calculated.
But in this case I load acting is parallel. the load acting is 3286N
Please guide me in solving this problem
Thanks
Please help me in solving this problem.
I need to calculate the dia of the Allen screw.
I have an assembly (2 parts).
Hydraulic fluid is passing thru the drilled hole.
I need to calculate the dia of the Allen screw (for fastening 2 plates).
The load is acting parallel to the fluids flow.
If the load is acting vertically I know the calculation to get the dia of the Allen screw.
In this case the load is parallel.
If the load is vertical the total load is divided be the number of bolts, which gives the load acting on each bolt, from that cross sectional area is calculated and from the Area dia of the bolt is calculated.
But in this case I load acting is parallel. the load acting is 3286N
Please guide me in solving this problem
Thanks
Attachments
Last edited: