Azael
- 257
- 1
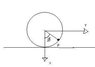
As in the attached picture.
A cylindrical shell with mass M can roll without gliding on a horizontal plane
In the cylindrical shell a particle ,p, with mass m can glide without friction.
At the beginning there is no motion and the angle to the particles position is \phi=\frac{\pi}{2}
I am suposed to find the movement of the center of the circle as a function of the angle \phi
Im not sure how I should start.
The potential energy of the system is, if I place the plane of reference on the level of the horizontal plane.
V=mgR(1-cos\phi)
Now this problem obviously only has one degree of freedom and that is the angle \phi
But if I want to construct a lagrangian I must use two degres of freedom. The rotation angle of the cylinder \alpha and the angle to the particle p \phi. Because I don't know how \alpha and \phi are connected. Is this the correct thinking?
In that manner I get this equation
L=T-V=\frac{3}{4}MR^2\dot{\alpha}^2+\frac{1}{2}m[\dot{\alpha}^2 R^2 + R^2\dot{\phi}^2 + \dot{\alpha}^2 R^2 sin\phi ] - mgR(1-cos\phi )
Should I use this and solve the two lagrande equations
\frac {d}{dt} \frac{dL}{d\dot{\alpha}}-\frac{dL}{d\alpha}=0
\frac {d}{dt} \frac{dL}{d\dot{\phi}}-\frac{dL}{d\phi}=0
Im not sure if this will give me any answere though? It feels like I should express \alpha in \phi before I even do the lagrangian. Am I on the right track?
A cylindrical shell with mass M can roll without gliding on a horizontal plane
In the cylindrical shell a particle ,p, with mass m can glide without friction.
At the beginning there is no motion and the angle to the particles position is \phi=\frac{\pi}{2}
I am suposed to find the movement of the center of the circle as a function of the angle \phi
Im not sure how I should start.
The potential energy of the system is, if I place the plane of reference on the level of the horizontal plane.
V=mgR(1-cos\phi)
Now this problem obviously only has one degree of freedom and that is the angle \phi
But if I want to construct a lagrangian I must use two degres of freedom. The rotation angle of the cylinder \alpha and the angle to the particle p \phi. Because I don't know how \alpha and \phi are connected. Is this the correct thinking?
In that manner I get this equation
L=T-V=\frac{3}{4}MR^2\dot{\alpha}^2+\frac{1}{2}m[\dot{\alpha}^2 R^2 + R^2\dot{\phi}^2 + \dot{\alpha}^2 R^2 sin\phi ] - mgR(1-cos\phi )
Should I use this and solve the two lagrande equations
\frac {d}{dt} \frac{dL}{d\dot{\alpha}}-\frac{dL}{d\alpha}=0
\frac {d}{dt} \frac{dL}{d\dot{\phi}}-\frac{dL}{d\phi}=0
Im not sure if this will give me any answere though? It feels like I should express \alpha in \phi before I even do the lagrangian. Am I on the right track?
Attachments
Last edited: