mcintyre_ie
- 66
- 0
Hey,
I’d appreciate some help with this question. Here’s a diagram:
Diagram
And the question:
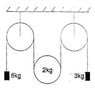
A moveable pulley of mass 2Kg is suspended on a light inextensible string between two fixed pulleys as shown and masses of 6kg and 3kg are asttached to the ends of the string. If the system is released from rest:
(I) Show in a diagram the forces acting on each of the masses.
(II) Find the acceleration of the moveable pulley and the tension in the string.
(III) If initially the moveable pulley had been replaced by another of mass m, find m, given that the moveable pulley remains at rest while the other two masses are in motion
I’m a bit confused about the accelerations of each particle and the pulley. From what I understand, the 6kg particle will move downwards, and the pulley and 3kg particle will move upwards. I’m assuming that some particle (probably the pulley?) will have a different acceleration to the others, maybe twice that of the others? I’m just lost as to what the accelerations are.
(I)Should be fine if I can find the accelerations.
(II)Should be ok too, once I have the accelerations and then use F=MA.
(III)Seems complicated, and I’m feeling I’ll probably have difficulty.
So, any advice on the accelerations and part (III) would be appreciated.
Thanks in advance.
I’d appreciate some help with this question. Here’s a diagram:
Diagram
And the question:
A moveable pulley of mass 2Kg is suspended on a light inextensible string between two fixed pulleys as shown and masses of 6kg and 3kg are asttached to the ends of the string. If the system is released from rest:
(I) Show in a diagram the forces acting on each of the masses.
(II) Find the acceleration of the moveable pulley and the tension in the string.
(III) If initially the moveable pulley had been replaced by another of mass m, find m, given that the moveable pulley remains at rest while the other two masses are in motion
I’m a bit confused about the accelerations of each particle and the pulley. From what I understand, the 6kg particle will move downwards, and the pulley and 3kg particle will move upwards. I’m assuming that some particle (probably the pulley?) will have a different acceleration to the others, maybe twice that of the others? I’m just lost as to what the accelerations are.
(I)Should be fine if I can find the accelerations.
(II)Should be ok too, once I have the accelerations and then use F=MA.
(III)Seems complicated, and I’m feeling I’ll probably have difficulty.
So, any advice on the accelerations and part (III) would be appreciated.
Thanks in advance.