- #1
aatari
- 73
- 3
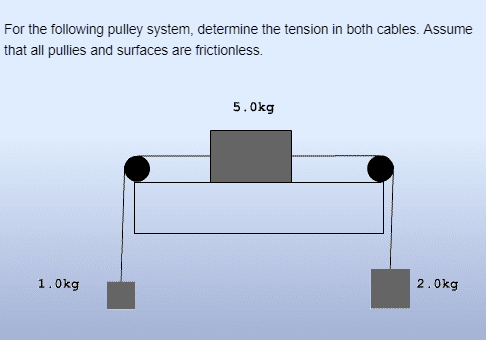
Hi guys, could someone please have a look at my solution and let me know if it makes any sense.
N/A
[/B]
Homework Statement
Homework Equations
N/A
"Review My Homework Solution" is a service or platform where students can submit their homework solutions for feedback and review by a qualified individual, typically a tutor or educator.
Using "Review My Homework Solution" can help you improve your understanding of the subject matter and identify any mistakes or areas for improvement in your homework solution. It can also save you time and effort by providing a second set of eyes on your work.
Typically, you will submit your homework solution through the platform and a qualified reviewer will assess it and provide feedback and suggestions for improvement. Some platforms may also offer real-time or interactive review sessions.
No, using "Review My Homework Solution" is not considered cheating as long as you are submitting your own work and using the feedback to improve your understanding and skills. However, it is important to check with your school or instructor to ensure that using such a service is allowed.
To make the most out of "Review My Homework Solution", it is important to carefully review the feedback provided by the reviewer and use it to improve your understanding and skills. You can also ask questions and seek clarification on any areas that you are unsure about.