afromanam
- 16
- 0
so now I'm undestanding a little bit more, but I'm still confused...
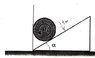
1) a momentum of 96 Nm is applied to the cylinder. The radius of the cylinder is 1 m. \mu_{A} = \mu_{C} = 0.25 The weight of the cylinder is 100 N. What is the minimum vale of \mu_B so the ramp moves to the right?. Weight of the ramp = 400 N. point B is the contact point between cylinder and the ramp.
My starting system of equations is:
96 \ N = F_{B} + F_{A}
Forces acting on the cylinder:
\sum{F_x} = -N_{B}\sin30 - F_{B}\cos30 + N_{A} = 0
\sum{F_y} = F_{A} + N_{B}\cos30 - F_{B}\sin30 - W_{cylinder} = 0
Forces acting on the ramp
\sum{F_x} = F_{B}\cos30 + N_{B}\sin30 - F_{C} = 0
\sum{F_y} = F_{B}\sin30 - N_{B}\cos30 +N_{C} - W_{ramp} = 0
From there, i go all the way to:
\mu_{B} = 0.55518
so far so good?, or I'm missing something? please refer to attachment 1
2) the body A 'weighs' 2500 kg. and body B 'weighs' 500 kg. \mu_{S} between A and B and between B and the ground is 0,2; and between A and the high surface is 0,5. Find the minimum required force P to start the movement of body B to right. Consider all the posibilities.
Ok, so when they say 'consider all the posibilities' i assumed that they meant that either x = z or x \neq z.
from there
forces acting on body A
\sum{F_X} = F_{A} = F_{C}
\sum{F_Y} = W_{A} = N_{A} + N_{C}
forces acting on body B
\sum{F_X} = P = F{_B} - F_{A}
\sum{F_Y} = N_{B} = N_{A} + W_{B}
\sum{M_{center \ of \ body \ A}}=\left\{\begin{array}{cc}N_{A} = N_{C},&\mbox{ if }<br /> x = z\\\frac{N_{A}}{N_{C}} = \frac{d_{2}}{d_{1}}, & \mbox{ if } x\neq z\end{array}\right.
\sum{M_{point \ A}}=\left\{\begin{array}{cc}\frac{W}{2} = N_{C} \ \mbox{(which, from previous balance of momentum)} = N_{A},&\mbox{ if }<br /> x = z\\N_{C} = \frac{d_{1}W_{B}}{d_{1}+d_{2}}, N_{A} = \frac{d_{2}W_{B}}{d_{1} + d_{2}}& \mbox{ if } x\neq z\end{array}\right.
so in both cases, i end up with P = 981 N, but as you can see \sum{F_X} of body A can not be satisfied if we were to satisfy also the \sum{M}, when x = z
3) I'm really growing fond of this Latex typesetting. I've seen quite a lot software for writing documents with Latex. which one do you recommend the most, for writing papers and/or a thesis?
thanks in advance for any help you can give me
1) a momentum of 96 Nm is applied to the cylinder. The radius of the cylinder is 1 m. \mu_{A} = \mu_{C} = 0.25 The weight of the cylinder is 100 N. What is the minimum vale of \mu_B so the ramp moves to the right?. Weight of the ramp = 400 N. point B is the contact point between cylinder and the ramp.
My starting system of equations is:
96 \ N = F_{B} + F_{A}
Forces acting on the cylinder:
\sum{F_x} = -N_{B}\sin30 - F_{B}\cos30 + N_{A} = 0
\sum{F_y} = F_{A} + N_{B}\cos30 - F_{B}\sin30 - W_{cylinder} = 0
Forces acting on the ramp
\sum{F_x} = F_{B}\cos30 + N_{B}\sin30 - F_{C} = 0
\sum{F_y} = F_{B}\sin30 - N_{B}\cos30 +N_{C} - W_{ramp} = 0
From there, i go all the way to:
\mu_{B} = 0.55518
so far so good?, or I'm missing something? please refer to attachment 1
2) the body A 'weighs' 2500 kg. and body B 'weighs' 500 kg. \mu_{S} between A and B and between B and the ground is 0,2; and between A and the high surface is 0,5. Find the minimum required force P to start the movement of body B to right. Consider all the posibilities.
Ok, so when they say 'consider all the posibilities' i assumed that they meant that either x = z or x \neq z.
from there
forces acting on body A
\sum{F_X} = F_{A} = F_{C}
\sum{F_Y} = W_{A} = N_{A} + N_{C}
forces acting on body B
\sum{F_X} = P = F{_B} - F_{A}
\sum{F_Y} = N_{B} = N_{A} + W_{B}
\sum{M_{center \ of \ body \ A}}=\left\{\begin{array}{cc}N_{A} = N_{C},&\mbox{ if }<br /> x = z\\\frac{N_{A}}{N_{C}} = \frac{d_{2}}{d_{1}}, & \mbox{ if } x\neq z\end{array}\right.
\sum{M_{point \ A}}=\left\{\begin{array}{cc}\frac{W}{2} = N_{C} \ \mbox{(which, from previous balance of momentum)} = N_{A},&\mbox{ if }<br /> x = z\\N_{C} = \frac{d_{1}W_{B}}{d_{1}+d_{2}}, N_{A} = \frac{d_{2}W_{B}}{d_{1} + d_{2}}& \mbox{ if } x\neq z\end{array}\right.
so in both cases, i end up with P = 981 N, but as you can see \sum{F_X} of body A can not be satisfied if we were to satisfy also the \sum{M}, when x = z
3) I'm really growing fond of this Latex typesetting. I've seen quite a lot software for writing documents with Latex. which one do you recommend the most, for writing papers and/or a thesis?
thanks in advance for any help you can give me
Attachments
Last edited: