Lachlan1
- 21
- 0
Homework Statement
this example is in the txtbook so i know the answer, but i don't really get the second part.
The road needs to be at a banked angle so the car traveling at 13.4m/s can go around with no friction needed, the radius of the corner is 35m.
Homework Equations
the given contructed equations are
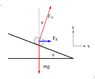
Fr=nsinө = (mv^2)/r i get this part, just the horizontal component of the normal force, which is the centripedal force.
then they use
Fy=ncosө – mg = 0
which i can see from the diagram is the vertical component of the normal force, less the weight force of the car. Why do they use this though?
they then divide the two equations.
The Attempt at a Solution
i got the first equation, and initially tried to write n, the normal force as mgcosө, and then substitute it into the first equation. Why is this not the normal force? like for an inclined plane example? and why do they subtract the car weight force from the verticle component of the normal force?
thanks