KKazaniecki
- 12
- 0
1. Homework Statement The system shown in the diagram contains two blocks, of masses 1.9 kg and 5.7 kg, connected by a light string over a pulley of radius 0.15 m and rotational inertia 2.8 kg m 2 . The block of mass 5.7 kg is free to slide on a horizontal frictionless surface and the pulley is free to rotate on a frictionless fixed horizontal axle passing through its center. Find the magnitude of the angular acceleration α of the pulley once the system is released from rest. The string connecting the blocks does not slip on the pulley. Enter your answer in rad/s 2 and use g = 9.8 m/s 2 .
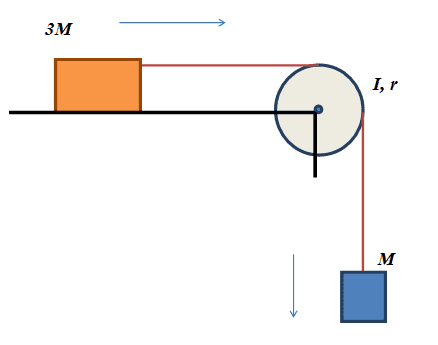
2. Homework Equations
τ=Torque
t=tension
A=linear acceleration
aΘ=Angular acceleration
r=radius
τ=I*aΘ
A=r*aΘ
F=A*m
3. The Attempt at a Solution
box with mass m is box 1
box with mass 3m is box 2
ok so, drawing a FBD of both boxes we get. F1=m*g-t=m*a. t=m*g-m*a.
and F2=3*m*a=t. Since tension and acceleration is the same throughout.
m*g-m*a=3*m*a. So we get a=g/4.
Now since we know acceleration we can use it in a equation.
τ=r*t.where t= (m*g-m*a) or (3*m*a).
rearranging the formula τ=I*aΘ.
we substitute the variables in. we get τ/I=aΘ. = r*(3*m*a)/I = aΘ.
and we know all the variables there substituting them we get. 0.15*(3*1.9*2.45)/2.8 = aΘ.
and the final answer is aΘ= 0.748125.
but when I put it down as the answer it marks me incorrect. Could someone help me out to see where I went wrong ? thank you :)
2. Homework Equations
τ=Torque
t=tension
A=linear acceleration
aΘ=Angular acceleration
r=radius
τ=I*aΘ
A=r*aΘ
F=A*m
3. The Attempt at a Solution
box with mass m is box 1
box with mass 3m is box 2
ok so, drawing a FBD of both boxes we get. F1=m*g-t=m*a. t=m*g-m*a.
and F2=3*m*a=t. Since tension and acceleration is the same throughout.
m*g-m*a=3*m*a. So we get a=g/4.
Now since we know acceleration we can use it in a equation.
τ=r*t.where t= (m*g-m*a) or (3*m*a).
rearranging the formula τ=I*aΘ.
we substitute the variables in. we get τ/I=aΘ. = r*(3*m*a)/I = aΘ.
and we know all the variables there substituting them we get. 0.15*(3*1.9*2.45)/2.8 = aΘ.
and the final answer is aΘ= 0.748125.
but when I put it down as the answer it marks me incorrect. Could someone help me out to see where I went wrong ? thank you :)