Angular frequency of a non-sinusoidal pulse

[Intoto]

Hey all, so I’ve been learning nonlinear acoustics and have encountered a conceptual hurdle in my studies. When using a model, such as a form of the classical Burgers equation, to propagate sound waves, you generally have a “characteristic angular frequency” in the equation (often represented by omega). For a simple sine wave, this is very easy to understand. However, let’s say the wave to be propagated is a discrete, non-sinusoidal pulse.

I have attached an illustration below as an example of what I am talking about.

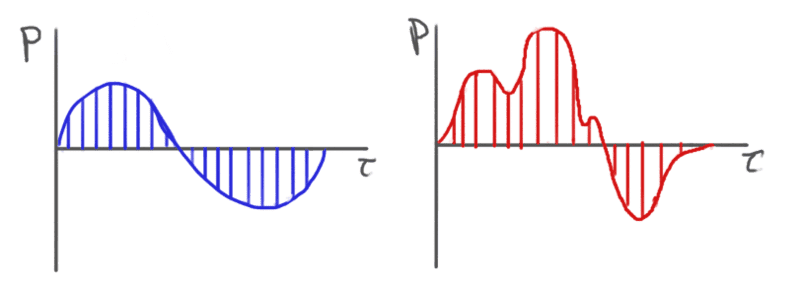
(Excuse my art skills, blue is supposed to be a uniformly sampled sin wave and red is supposed to be a uniformly sampled pulse.)

I am unsure of what the “characteristic angular frequency” is supposed to represent when using a wave such as the single, non-sinusoidal pulse. I am assuming that it may require the use of Fourier transforms (which I am vaguely familiar with), but I am unsure of what I would even be looking for (e.g. a fundamental frequency, or perhaps a different frequency at every point in the waveform).

Any insight would be greatly appreciated.

 

[anorlunda]

You are correct. You could use Fourier analysis to break it into a sum of terms, each with a different frequency. But then each term would have its own angular velocity. So the question back to you is, "what do you think the significance of “characteristic angular frequency” is for the case of interest?

 

[Intoto]

I am not entirely sure how to respond to the question regarding the significance of the angular frequency, but I will try. The angular frequency of a wave is commonly encountered in many equations in nonlinear acoustics. An example of this would be the nondimensionalization of the classical Burgers equation.

Without getting into details, time t in the Burgers equation is commonly nondimensionalized through the use of a characteristic angular frequency:

tau = t * omega .

In this case tau is the dimensionless time and omega is the characteristic angular frequency. You can see the nondimensionlized equation containing the characteristic angular frequency terms above.

Most texts do not comment on this matter, but in one of the texts I have gone through, they mentioned that for pulses the angular frequency may correspond to the dominant spectral component in the source waveform. I have not been able to determine what exactly they mean by dominant spectral component. Would this just correspond to the highest amplitude in a Fourier transform?

 

[rumborak]

Doesn't the whole concept of describing arbitrary waveforms as a sum of sinusoids fall apart when you consider nonlinear systems? The reason you can do all these convenient acrobatics of angular frequencies etc is because sinusoids are the solution to the *linear* wave equation. The moment nonlinearities appear you can no longer view these frequencies as independent, and you have to stick to the differential equation and its numerical solutions.

 

[FactChecker]

I have not been able to determine what exactly they mean by dominant spectral component. Would this just correspond to the highest amplitude in a Fourier transform?

Yes.