quickclick330
- 82
- 0
Two small objects each of mass m = 0.6 kg are connected by a lightweight rod of length d = 1.3 m (Figure 9.60). At a particular instant they have velocities whose magnitudes are v1 = 27 m/s and v2 = 67 m/s and are subjected to external forces whose magnitudes are F1 = 51 N and F2 = 32 N. The distance h = 0.3 m, and the distance w = 0.5 m. The system is moving in outer space.
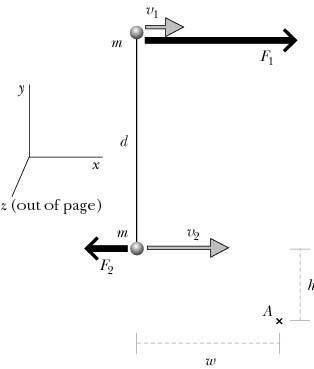
(a) What is the total (linear) momentum total of this system?
(b) What is the velocity cm of the center of mass?
(c) What is the total angular momentum A of the system relative to point A?
(d) What is the rotational angular momentum rot of the system?
(e) What is the translational angular momentum trans of the system relative to point A?
(f) After a short time interval t = 0.16 s, what is the total (linear) momentum total of the system?
Solved So far...
a)linear momentum = <.6 kg * 27 m/s + 0.6 kg * 27 m/s, 0, 0>
= <56.4, 0,0>
b) Vcm = Ptotal/Mtotal = <56.4, 0,0>/1.2 kg = 47.0
c) stuck on this one...
I'm having trouble understanding what exactly to use for the angular momentum.
LA = r X p (both vectors) but i don't know what to use for r, the position of the center of mass??
Thanks :-)
(a) What is the total (linear) momentum total of this system?
(b) What is the velocity cm of the center of mass?
(c) What is the total angular momentum A of the system relative to point A?
(d) What is the rotational angular momentum rot of the system?
(e) What is the translational angular momentum trans of the system relative to point A?
(f) After a short time interval t = 0.16 s, what is the total (linear) momentum total of the system?
Solved So far...
a)linear momentum = <.6 kg * 27 m/s + 0.6 kg * 27 m/s, 0, 0>
= <56.4, 0,0>
b) Vcm = Ptotal/Mtotal = <56.4, 0,0>/1.2 kg = 47.0
c) stuck on this one...
I'm having trouble understanding what exactly to use for the angular momentum.
LA = r X p (both vectors) but i don't know what to use for r, the position of the center of mass??
Thanks :-)