Angular velocity of a loop after being struck by bullet

[haruspex]

Why does the bullet initially have an R value?

Do you mean, why does it have initial angular momentum mvR?

 

[Orodruin]

Yes why does the bullet initially have angular momentum, if it is traveling linearly

Anything moving linearly on a path offset from the reference point has angular momentum.

assuming it is a point mass with some radius r,

This is nonsense. A point mass is a point and has no radius.

why does it cancel out with the radius of the loop

It … doesn’t?

 

[Elj]

Anything moving linearly on a path offset from the reference point has angular momentum.This is nonsense. A point mass is a point and has no radius.It … doesn’t?

alright then can you explain how to solve it, Im genuinely confused

 

[Orodruin]

alright then can you explain how to solve it, Im genuinely confused

I already did. See #22 and #23.

 

[PeroK]

alright then can you explain how to solve it, Im genuinely confused

Using conservation of angular momentum about the centre of mass, which is $\frac R 2$ below the centre of the hoop:
$$L = mv\frac R 2 = m(\frac R 2)^2 \omega + I \omega = (\frac{mR^2}{4} + I)\omega$$Where $I$ is the moment of inertia of the hoop about the centre of mass of the system. Using the parallel axis theorem we have:
$$I = mR^2 + m(\frac R 2)^2 = \frac{5mR^2}{4}$$This gives:
$$\frac{6mR^2}{4}\omega = mv\frac R 2$$$$\omega = \frac{v}{3R}$$

 

[Orodruin]

Using conservation of angular momentum about the centre of mass, which is $\frac R 2$ below the centre of the hoop:
$$L = mv\frac R 2 = m(\frac R 2)^2 \omega + I \omega = (\frac{mR^2}{4} + I)\omega$$Where $I$ is the moment of inertia of the hoop about the centre of mass of the system. Using the parallel axis theorem we have:
$$I = mR^2 + m(\frac R 2)^2 = \frac{5mR^2}{4}$$This gives:
$$\frac{6mR^2}{4}\omega = mv\frac R 2$$$$\omega = \frac{v}{3R}$$

I should add that the only reason I did not do it like this is that the OP already did that. My treatment in #22 and #23 was based on conservation of linear momentum and the angular momentum relative to a point that is not the center of mass of the system - the point being to show that it is also possible, but more involved.

 

[haruspex]

I should add that the only reason I did not do it like this is that the OP already did that. My treatment in #22 and #23 was based on conservation of linear momentum and the angular momentum relative to a point that is not the center of mass of the system - the point being to show that it is also possible, but more involved.

Right, but @Elj is not the OP, and was blocked at an earlier point: the understanding that linear momentum also acts as angular momentum about any axis not in the line of motion (which you addressed in post #32).

@Elj, if you are still struggling with that, it's like forces and torques. A linear force also acts as a torque about any axis not in its line of action.
Having explained that, the next step should be for you to show some attempt.

 

[Orodruin]

Right, but @Elj is not the OP, and was blocked at an earlier point: the understanding that linear momentum also acts as angular momentum about any axis not in the line of motion (which you addressed in post #32).

In #36 I was just clarifying why my solution is more involved that the one presented by @PeroK - noting that I would certainly not suggest doing it that way in the normal case - but did so for the benefit of the OP.

 

[brochesspro]

Consider a rigid body with masses $m_i$ that have time dependent positions $\vec x_i$. For such a body, the velocity field may be described by
$$
\vec v = \vec v_r + \vec \omega \times (\vec x - \vec x_r)
$$
where the $r$ subscript denotes a reference point. By definition, the angular momentum relative to the reference point is
$$
\vec L_r = \sum_i m_i (\vec x_i - \vec x_r) \times \vec v_i
= \sum_i m_i (\vec x_i - \vec x_r) \times(\vec v_r + \vec \omega \times (\vec x_i - \vec x_r)).
$$
We now use that $\sum_i m_i \vec x_i = M \vec x_{cm}$ defines the center of mass (with $M$ being the total mass):
$$
\vec L_r = M (\vec x_{cm} - \vec x_r) \times \vec v_r + I_r (\vec \omega)
$$
where $I_r$ is the moment of inertia tensor relative to $\vec x_r$. The first term is zero in the the following cases:

• $\vec v_r = 0$: The reference point is chosen such that it has zero instantaneous velocity.
• $\vec x_r = \vec x_{cm}$: The reference point is the center of mass.
• $(\vec x_{cm} - \vec x_r)\times \vec v_r = 0$: The offset from the CoM to the reference point is parallel to $\vec v_r$.

None of the above is applicable to the center of the hoop in your case so you cannot ignore the first term for the angular momentum after the collision.

I didn't get the 1st line. $\vec v = \vec v_r + \vec \omega \times (\vec x - \vec x_r)$ How do we know whether or not the object moves radially to the reference point?
Also, I did not get how you obtained the 3rd line from the 2nd line.

If you are saying the the hoop moves inertially, then that is wrong.

I am not familiar with the term "moves inertially". Does it mean that the object moves with uniform velocity?

Why does the bullet initially have an R value? assuming that mvr=(12/4mr^2)ω

Because it is at a distance R from the centre of the loop.
Also, I apologise for my late response to all the helpful messages. I was studying chemistry for my college entrances and it was really hard to switch my mind to physics mode.
Also, I tried another approach to solve this question, but I still get an incorrect, albeit different answer. I will post my procedure in a couple of hours.

 

[Orodruin]

How do we know whether or not the object moves radially to the reference point?

It doesn’t necessarily. The $r$ subscript is for $r$eference, not radial. Note the vector arrow on top of $\vec v_r$, it is a vector, not a vector component.

Also, I did not get how you obtained the 3rd line from the 2nd line.

I used the definition of the center of mass as a sum over all particles. Many of the factors in the expression are constant and can therefore be taken out of the sum.

I also used the definition of the moment of inertia tensor relative to the reference point.

 

[PeroK]

I am not familiar with the term "moves inertially". Does it mean that the object moves with uniform velocity?

Yes. I meant that the centre of mass of the hoop, which is in fact its centre, does not move inertially, but orbits the centre of mass of the hoop/bullet system.

That's why I encouraged you to draw some diagrams. To get an insight into the "wobbly" motion of the hoop.

 

[brochesspro]

It doesn’t necessarily. The r subscript is for reference, not radial. Note the vector arrow on top of v→r, it is a vector, not a vector component.

I understood that, but my doubt was how we would know the radial velocity of the object with reference to the reference point. Or do we not need it as it is not needed for the calculation of the angular momentum vector?

I used the definition of the center of mass as a sum over all particles. Many of the factors in the expression are constant and can therefore be taken out of the sum.

Okay, I shall try it.

That's why I encouraged you to draw some diagrams. To get an insight into the "wobbly" motion of the hoop.

Got it, but how will it help to solve the problem?
Also, here is my new procedure.

 

[Orodruin]

I understood that, but my doubt was how we would know the radial velocity of the object with reference to the reference point. Or do we not need it as it is not needed for the calculation of the angular momentum vector?

You have to silve for $\vec v_r$ from the conservation laws just as you have to solve for $\omega$. In the solution I just expressed it in terms of $\omega$ using the linear momentum conservation in order to eliminate it from the angular momentum conservation. That way the angular momentum conservation was expressable in $\omega$ only and it could be solved for. As the question did not ask about the linear velocity (only angular), I did not care about taking the time to explicitly express $\vec v_r$ in terms of the input.

 

[Orodruin]

Also, here is my new procedure.

Please use the forum LaTeX features rather than posting images. Images are impossible to quote relevant parts of.

I do not understand what you have done to write down the angular momentum conservation. The correct procedure is in #23.

 

[haruspex]

I understood that, but my doubt was how we would know the radial velocity of the object with reference to the reference point. Or do we not need it as it is not needed for the calculation of the angular momentum vector?

Okay, I shall try it.

Got it, but how will it help to solve the problem?
Also, here is my new procedure.
View attachment 337922

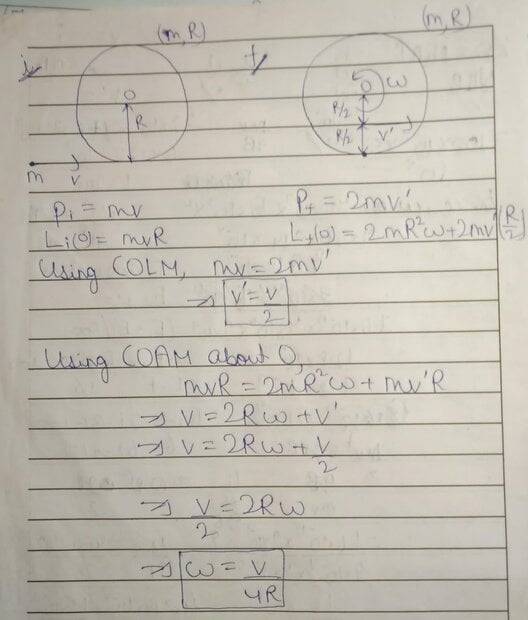
I think you have confused yourself by, on the one hand, taking moments about O and, on the other, defining v' as the velocity of the CoM.
For clarity, I will refer to the original position of the centre of the hoop as the fixed point O and the moving centre as O'.
Since, for angular momentum purposes, you are treating the subsequent motion of the bullet as the sum of rotation about O' and the linear motion of O', and you have already accounted for the rotational contribution of the bullet about O' in $2mr\omega^2$, you just need the contribution from the bullet in respect of the linear motion of O'.
What is the velocity of O'?

 

[brochesspro]

you just need the contribution from the bullet in respect of the linear motion of O'.

I do not get this part.

What is the velocity of O'?

How do we find that out?

Please use the forum LaTeX features rather than posting images. Images are impossible to quote relevant parts of.

Sorry, I did it due to time constraints, I shall take care from next time.

I also used the definition of the moment of inertia tensor relative to the reference point.

Could you please confirm if I am correct here, after I split the terms $\vec v_r$ and the term $\vec \omega \times (\vec x_i - \vec x_r)$ with the vector product, I get a vector triple product in the 2nd term. But since the vectors $\vec \omega$ and $\vec x_i - \vec x_r$ are always perpendicular(since we are dealing with 2D motion), their dot product is zero, and then we are left with this guy, $I_r (\vec \omega)$. I still do not get the centre of mass part though.

 

[Orodruin]

Could you please confirm if I am correct here, after I split the terms $\vec v_r$ and the term $\vec \omega \times (\vec x_i - \vec x_r)$ with the vector product, I get a vector triple product in the 2nd term. But since the vectors $\vec \omega$ and $\vec x_i - \vec x_r$ are always perpendicular(since we are dealing with 2D motion), their dot product is zero, and then we are left with this guy, $I_r (\vec \omega)$. I still do not get the centre of mass part though.

There is no dot product. Just cross products. The first term is very relevant.

 

[haruspex]

How do we find that out?

Calculate it from v', r and ω. Call it v".
For the purpose of finding the angular momentum about O, you can think of the motion of the hoop+bullet system immediately after impact as the sum of the linear motion of O' (velocity v") and a rotation about O'. For each of hoop and bullet, each of these motions makes a contribution to the angular momentum, potentially making four terms in all.
For the hoop, the linear motion of the mass centre is in a line through O, so that term is zero. The rotational term is $mr^2\omega$.
The rotational term for the bullet is also $mr^2\omega$, as you posted.
That leaves the linear term for the bullet: a mass m moving at velocity v" along a path that is distance r from O at the nearest: $mv''r$

 

[Orodruin]

As for the com issue. Consider
$$
\sum_i m_i (\vec x_i - \vec x_r) \times \vec v_r
=
M \left[ \underbrace{\frac 1M \sum_i m_i \vec x_i}_{\equiv \vec x_{cm}} - \vec x_r \frac 1M \underbrace{\sum_i m_i}_{\equiv M} \right] \times \vec v_r
=
(M \vec x_{cm} - M \vec x_r)\times \vec v_r
$$

 

[brochesspro]

As for the com issue. Consider
$$
\sum_i m_i (\vec x_i - \vec x_r) \times \vec v_r
=
M \left[ \underbrace{\frac 1M \sum_i m_i \vec x_i}_{\equiv \vec x_{cm} - \vec x_r \frac 1M \underbrace{\sum_i m_i}_{\equiv M} \right] \times \vec v_r
=
(M \vec x_{cm} - M \vec x_r)\times \vec v_r
$$

Could you please edit this message? It only shows the plain text, without the implementation of formatting.

 

[Orodruin]

Could you please edit this message? It only shows the plain text, without the implementation of formatting.

No. I have obviously tried. It is reported to staff.

 

[brochesspro]

There is no dot product.

When we expand the vector triple product, we get a linear combination of the vectors inside the cross product whose coefficients are in the form of dot product.

The first term is very relevant.

I know, and that is the very thing I fail to understand.

 

[Orodruin]

No. I have obviously tried. It is reported to staff.

Scrap that, I found the missing }

 

[Orodruin]

I get a vector triple product in the 2nd term.

When we expand the vector triple product,

You don’t need to expand it. It is the definition of $I_r(\vec \omega)$.

Edit: I mean, you can expand it to rewrite it as
$$
m\vec d \times [\vec \omega \times \vec d]
=
md^2 \vec \omega - \vec d (\omega\cdot \vec d) = md^2 \vec \omega
$$
for an expression more familiar in 2D.

 

[brochesspro]

As for the com issue. Consider
$$
\sum_i m_i (\vec x_i - \vec x_r) \times \vec v_r
=
M \left[ \underbrace{\frac 1M \sum_i m_i \vec x_i}_{\equiv \vec x_{cm}} - \vec x_r \frac 1M \underbrace{\sum_i m_i}_{\equiv M} \right] \times \vec v_r
=
(M \vec x_{cm} - M \vec x_r)\times \vec v_r
$$

Why can we take the Xr out of the Σ? Is it not variable? Since Vr represents its rate of change.

You don’t need to expand it. It is the definition of $I_r(\vec \omega)$.

Could you tell its definition?

 

[Orodruin]

Why can we take the Xr out of the Σ? Is it not variable?

The reference point is fixed.

Edit: Even if it were variable it is independent of $i$, which is what the sum is over…

Since Vr represents its rate of change.

No. It represents the velocity of the solid body at $\vec x_r$.

Could you tell its definition?

$$
I_r(\vec \omega) = \sum_i m_i (\vec x_i - \vec x_r)\times [\vec \omega \times (\vec x_i - \vec x_r)]
$$
…

 

[brochesspro]

No. It represents the velocity of the solid body at x→r.

Wait, $\vec x_r$ and $\vec v_r$ are not the position and the velocity of the reference point respectively? Then what do they mean?

 

[Orodruin]

Wait, $\vec x_r$ and $\vec v_r$ are not the position and the velocity of the reference point respectively? Then what do they mean?

Exactly what I said they mean in my last post.