Angular Velocity of Rotating Mass

[20930997]

1. Homework Statement

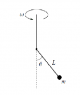
A solid sphere of mass m rotates uniformly in a horizontal circle suspended from a fixed
point on a cord of length L and negligible mass. The cord
makes an angle theta from the vertical. What is the angular
velocity?

2. Homework Equations

Torque= (Rotational Inertia)x(angular acceleration)


3. The Attempt at a Solution

Tried to mess around with a few things but ultimately got no-where so any help would be greatly appreciated.

 

[20930997]

This is the Diagram for the problem

 

[Hootenanny]

Welcome to Physics Forums.

I would suggest that you draw a free body diagram, identifying all the forces acting on the mass.

 

[20930997]

thanks for the welcome,

so there would be a tension force through the cord, a gravitational force acting straight down and a centripetal force. am i missing anything?

 

[Hootenanny]

thanks for the welcome,

so there would be a tension force through the cord, a gravitational force acting straight down and a centripetal force. am i missing anything?

No, that's spot on. So, what can you say about the horizontal and vertical components of the forces acting on the mass?

 

[20930997]

the vertical components sum to zero.
does the horizontal component of the tension= the centripetal force?

 

[Hootenanny]

the vertical components sum to zero.
does the horizontal component of the tension= the centripetal force?

Correct!

 

[20930997]

ok so i got to
tan(theta)=(v^2)/rg where r= Lsin(theta)

i was thinking solve for v and then use Angular velocity=v(r)

is this heading in the right direction?

 

[Hootenanny]

ok so i got to
tan(theta)=(v^2)/rg where r= Lsin(theta)

i was thinking solve for v and then use Angular velocity=v(r)

is this heading in the right direction?

Looks okay to me.

 

[20930997]

ok so i got angular velocity= g/Lcos(theta)

but the answers tell me that it should be the sqrt of that.
im a bit lost as to where i have made my mistake :S

 

[20930997]

oh wait i forgot to square both sides of the equation!

thanks for your help!

 

[Hootenanny]

ok so i got angular velocity= g/Lcos(theta)

but the answers tell me that it should be the sqrt of that.
im a bit lost as to where i have made my mistake :S

So you have

\frac{v^2}{r} = g\tan\theta

And you know that v = \omega r. Thus,

\omega^2 r = g\tan\theta

Do you follow and can you take it from here?

 

[Hootenanny]

oh wait i forgot to square both sides of the equation!

thanks for your help!

Ahh! Never-mind!

No problem, it was a pleasure!