Angular Velocity Problem — a Piston and a Crank

[JohnnyS]

Homework Statement

I have been set this question and I am struggling with parts b and c. I think I am nearly there but can't quite get over the line. Please could someone give me a nudge in the right direction.
[/B]
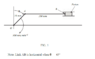
1. (a) For the mechanism shown in FIGURE 1 determine for the angle
θ = 45°:
(i) the velocity of the piston relative to the fixed point O (VBO)
(ii) the angular velocity of AB about point A (i.e. ωAB)
(iii) the acceleration of point B relative to A (aBA).

(b) Determine the value of the angle θ (measured from vertical) when:
(i) the velocity of point B = 0
(ii) the angular velocity of link AB a maximum.

(c) What is the maximum angular velocity of link AB?

The Attempt at a Solution

1i) VBO = 1.1 ms-1

ii) ωAB = 5.55 rads-1

iii) 13.6cm and 40.8ms-2

The above I am happy with my answers which is why I have not included all my calculations and diagrams. Below is my attempt at the remaining questions.

1b)i) When the velocity of B is 0 ms-1 the piston must be either fully extended or fully retracted.
Offset length = cos45° x 50mm
= 35.36mm

Rod length at full extension = 200mm + 50mm
= 250mm

sinØ1 = 35.36
250
= sin-1(0.14144)
Ø1 = 8.13°
Ø = 90° – Ø1
= 90 – 8.13

Ø = 81.87°

When the rod is fully retracted the angle will be 270° – 8.13° = 261.87°

1b)ii)The angular velocity of link AB will be at a maximum when it is perpendicular to either the fully retracted or fully extended rod. Ø = 90° + 8.13° = 98.13°

1b)iii)

ωAB = VBA VBA = SinØ x VAO
lAB = Sin(98.13°) x 1.571
= 1.555 = 1.555ms-1
0.2

ωAB = 7.76 rad s-1 VAO = 1.571ms-1
Ø = 98.13°
lAB = 200mm = 0.2m

I am not looking for answers here just a nod in the right direction as I feel that I may have strayed off path a little here.

Thanks in advance for any help.

 

[haruspex]

1i) VBO = 1.1 ms-1

That only seems to be a component (horizontal or vertical) of the speed. You are asked for the whole velocity.

ii) ωAB = 5.55 rads-1

Yes.

iii) 13.6cm and 40.8ms-2

What is the 13.6cm? You are only asked for an acceleration, for which I get a much smaller answer.
Again, acceleration is a vector, so you should specify a direction.
Please post your working for this part.

 

[haruspex]

Ø = 81.87°

Right.

When the rod is fully retracted the angle will be 270° – 8.13°

I don't think so. Use the same method as for the previous part.

 

[haruspex]

1b)ii)The angular velocity of link AB will be at a maximum when it is perpendicular to either the fully retracted or fully extended rod.

Why? Are you sure this is guaranteed to happen?
It can help to consider extreme cases. What if AB is much longer than OA? What direction would A be moving in when the angular velocity of AB is maximised?

 

[JohnnyS]

Sorry for my delay I have been away for the weekend. Thank you for the help so far. Below I have added my calculations for question 1 and the relevant diagrams should be attached too.

1i)
VAO = lOA x ωOA
= 0.05 x 31.42
= 1.571ms-1

VBO = cosØ x VAO
= cos45° x 1.571

VBO = 1.11ms-1

1ii)
VBA = sinØ x VAO
= sin45° x 1.571
= 1.1109ms-1

ωAB = VBA
lAB
= 1.55
0.2

ωAB = 7.76 rad s-1

DIAGRAM 1

1iii)
(aBA)r = lAB x ωAB2
= 0.2 x 5.552
aBA = 6.16ms-2

(aAO)r = lOA x ωOA2
= 0.5 x 31.422
aBA = 49.36ms-2

From the acceleration diagram attached with a scale of 1cm = 3ms-2

(aBA)t = 11.6cm from diagram = 34.8ms-2

(aBO)t = 13.6cm from diagram = 40.8ms-2

With regards to when the rod is fully retracted I assumed that the angle would be the same but opposite. If i use the same method I get

sinØ1 = 35.36
150
= sin-1(0.23573)
Ø1 = 13.63°
Ø = 270° – Ø1
= 270 – 13.63

Ø = 256.37°

I think I am slightly confused here now with regards to the maximum angular velocity at link AB. I thought it would be when perpendicular to the rod at full retraction or extension? How can I show this? 'A' would be pushing the piston to the right would it not, when the angular velocity of AB is maximised?

 

[haruspex]

VBO = 1.11ms-1

I do apologise. i must have misread the question - twice!

1ii)
VBA = sinØ x VAO
= sin45° x 1.571
= 1.1109ms-1

ωAB = VBA
lAB
= 1.55
0.2

ωAB = 7.76 rad s-1

I'm confused. You originally answered 5.55 and I agreed. Your attached diagram also shows 5.55.

1iii)
(aBA)r = lAB x ωAB2
= 0.2 x 5.552
aBA = 6.16ms-2

Not following the algebra, but I agree that this is the radial acceleration.

(aAO)r = lOA x ωOA2
= 0.5 x 31.422
aBA = 49.36ms-2

Not following this at all. You write aBA with two meanings? What is the method behind your calculation of the tangential acceleration?
Seems to me you missed a sin(θ) factor.

I suggest a safer approach is to write the angle AB makes to the horizontal as φ, say, and obtain the general equation relating the two angles and the two lengths (r=OA, L=AB). You can then differentiate to obtain components of velocities and accelerations in x and y directions.
I feel sure that will help with part b.

 

[JohnnyS]

1ii) Sorry I seem to have combined 2 answers together when typing it up. This should as you say be:-
VBA = sinØ x VAO
= sin45° x 1.571
= 1.1109ms-1
ωAB = VBA / lAB
= 1.1109 / 0.2
ωAB = 5.55 rad s-1

With regards to the question 1iii) I am not sure as to how to type in all the mathematical symbols so I used 'a' for acceleration so the radial acceleration at
BA = 6.16ms-2
Another typo in the next one which should read radial acceleration for AO = 49.36ms-2.
With regards to the tangential acceleration I have used the acceleration diagram drawn to a scale of 1cm = 3ms-2 to obtain the tangential acceleration BA =34.8ms-2 (11.6cm on the diagram) and tangential acceleration BO = 40.8ms-2 (13.6cm on the diagram).

 

[haruspex]

With regards to the tangential acceleration I have used the acceleration diagram drawn to a scale of 1cm = 3ms-2 to obtain the tangential acceleration BA =34.8ms-2 (11.6cm on the diagram) and tangential acceleration BO = 40.8ms-2 (13.6cm on the diagram).

Ok, but that is all invisible to me. I can only help if you use and post algebra.
Remember that the tangential acceleration of A wrt its rotation about B (an accelerating reference frame) is, in the diagram position, its vertical acceleration.

 

[Traposaurus]

Hey JohnnyS...How did you go about tackling the final couple of questions?

Determine the value of the angle θ (measured from vertical) when:
(i) the velocity of point B = 0
(ii) the angular velocity of link AB a maximum.

(c) What is the maximum angular velocity of link AB?

I think I've got the answer for (i) which is 2 separate angles, but I'm not sure where to start with the next 2 questions. There's no relevant equations or methods in the uni reading material so I'm a bit stumped.

 

[JohnnyS]

I have only just submitted my assignment so I don't know for sure if I have got this right but I have am pretty sure that the angualr velocity of AB is at maximum when it is perpendicular to the fully retracted / fully extended rod. So I just added the angle I calculated for the fully extended rod with 90°. Then for the next part I used the equation below. Like I say I don't know for sure if this is right as I haven t had my results yet but I will post again when I do to confirm if I was right or not. Hope this helps.
ωAB = VBA
lAB

 

[Traposaurus]

Thanks for that mate. Out of interest, why would the velocity be maximum when perpendicular to the fully extended/retracted angle?

I've always thought I was OK at maths but I do not understand velocity and vector diagrams etc at all. This whole module has really got me!

Interested to hear how you get on with the marking anyway.

 

[haruspex]

I have only just submitted my assignment

Then I feel free to post my solutions.
I will write r for OA, L for AB, ω for $\dot\theta$, and φ for the angle of AB above the horizontal.

For a(iii), the acceleration of point B relative to A when θ=45°:
Easier to think in terms of the accn of A relative to B.
A is moving vertically downwards rel to B at speed ωr sin(π/4).
A's acceleration is towards O, centripetally, at rω². This gives it a vertical acceleration (tangentially to B) of a_y=a_ABy=-rω²cos(π/4).
At the same time, it has a centripetal acceleration towards B of $\omega^2r^2\sin^2(\pi/4)/L=\frac{\omega^2r^2}{2L}$
Thus, as a vector, B's accn relative to A is
$-\frac{\omega^2r^2}{2L}\hat x+\frac{r\omega^2}{\sqrt 2}\hat y$.
With numbers: $-6.17\hat x+34.9\hat y$ m/s².

b(i) θ when the velocity of point B = 0
Clearly this is when the linkages align, θ+φ=π/2 or θ+φ=3π/2.
For θ+φ=π/2, (L+r)cos(θ)=r cos(π/4). θ=1.43 rad = 81.9°.
For θ+φ=3π/2, (L-r)cos(θ-π)=r cos(π/4). θ=4.47 rad = 256°.

b(ii) θ when the angular velocity of link AB a maximum.
B is a constant height above O:
(1) $L\sin(\phi)+r\cos(\theta)=r\cos(\pi/4)$
Differentiating..
$L\cos(\phi)\dot\phi=r\sin(\theta)\omega$
(2) $L\dot\phi=r\sin(\theta)\omega\sec(\phi)$
$L\ddot\phi=r\cos(\theta)\omega^2\sec(\phi)+r\sin(\theta)\omega\sec(\phi)\tan(\phi)\dot\phi$
At max $\dot\phi$:
$0=r\cos(\theta)\omega^2\sec(\phi)+r\sin(\theta)\omega\sec(\phi)\tan(\phi)\dot\phi$
$\omega=-\tan(\theta)\tan(\phi)\dot\phi$
$=-\tan(\theta)\tan(\phi)\sin(\theta)\omega\sec(\phi)r/L$
$-1=\tan(\theta)\sin(\theta)\frac{s}{1-s^2}\frac rL$, where $s = \sin(\phi)=(\cos(\pi/4)-\cos(\theta))\frac rL$
$s^2-1=\tan(\theta)\sin(\theta)s\frac rL$
$(\cos(\pi/4)-\cos(\theta))^2-\frac{L^2}{r^2}=\tan(\theta)\sin(\theta)(\cos(\pi/4)-\cos(\theta))$
$(\cos(\pi/4)-\cos(\theta))^2-\frac{L^2}{r^2}=\sec(\theta)\sin^2(\theta)(\cos(\pi/4)-\cos(\theta))$
$(\cos(\pi/4)-c)^2-\frac{L^2}{r^2}=\frac{1-c^2}c(\cos(\pi/4)-c)$, where c=cos(θ).
$(\frac 12-c\sqrt 2+c^2)c=c\frac{L^2}{r^2}+(1-c^2)(\cos(\pi/4)-c)$
$\frac 12c-c^2\sqrt 2+c^3=c\frac{L^2}{r^2}+\cos(\pi/4)-c-c^2\cos(\pi/4)+c^3$
$\frac 12c-c^2\sqrt 2=c\frac{L^2}{r^2}+\cos(\pi/4)-c-c^2\cos(\pi/4)$
$(\sqrt 2-1/\sqrt 2)c^2+(\frac{L^2}{r^2}-\frac 32) c +\cos(\pi/4)=0$
$c^2+(\frac{L^2}{r^2}-\frac 32)\sqrt 2 c +1=0$
c=-0.0489
θ=92.8°
Note that this means the peak angular velocity of AB is reached not merely after collinearity of the rods but even after A descends below the level of O.

(c) What is the maximum angular velocity of link AB?
(1) $L\sin(\phi)+r\cos(\theta)=r\cos(\pi/4)$
$\sin(\phi)=\frac rL(\cos(\pi/4)-\cos(\theta))$
With numbers:
sin(φ)=¼ 0.756
cos(φ)=±0.982
From (2) $\dot\phi=\frac rL\sin(\theta)\omega\sec(\phi)$=7.99 rad/sec

 

[Traposaurus]

I have only just submitted my assignment so I don't know for sure if I have got this right but I have am pretty sure that the angualr velocity of AB is at maximum when it is perpendicular to the fully retracted / fully extended rod. So I just added the angle I calculated for the fully extended rod with 90°. Then for the next part I used the equation below. Like I say I don't know for sure if this is right as I haven t had my results yet but I will post again when I do to confirm if I was right or not. Hope this helps.
ωAB = VBA
lAB

How did you get on in the end pal?