RadiationX
- 255
- 0
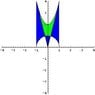
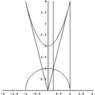
let Q be the solid that is outside both x^2 +y^2 +z^2=1 and z=2x^2 +2y^2 +2, yet inside z=4\sqrt{x^2 + y^2}
Could someone give me a little jump start on this problem? I would love a complete solution but anyhelp will do.
Could someone give me a little jump start on this problem? I would love a complete solution but anyhelp will do.