ElectroMaster88
- 5
- 3
- Homework Statement
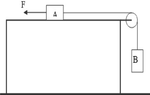
- Body A, which has a mass of 3 kg, is on a horizontal surface and is connected by a massless and frictionless string and pulley to body B, which is suspended in the air and has a mass of 2 kg. The coefficient of friction (static and kinetic) between body A and the horizontal surface is 0.2.
A horizontal force F is applied to body A to the left.
A. Calculate what the value of the force F should be in order for the frictional force between body A and the surface to be zero.
B. In what range of values should the force F be in order for the system to be in a static state? There are answers:
A. 20N
B. 14N ≤ F ≤ 26N
- Relevant Equations
- x=x0+v0t+at^2/2
v=v0+at
f=μ*N
N=mg
Newton's Second Law
I don't understand how to solve these, and I don't understand how an horizontal force can affect the friction force if it's defined by μ*N, and the additional force affect neither of those. I also don't understand how there is a range of possible forces that F can be to make the system static, if only one option can make the horizontal net force 0.
I am clearly missing something and I don't understand what.
I am clearly missing something and I don't understand what.