Bashyboy
- 1,419
- 5
Homework Statement
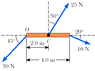
Calculate the net torque (magnitude and direction) on the beam in the figure below about the following axes.
(a) an axis through O, perpendicular to the page
(b) an axis through C, perpendicular to the page
Homework Equations
The Attempt at a Solution
I was able to solve part (b), but was unsuccessful with part (a). For part (a), I took note of the fact that the 30 N force applied at a 45 deg. angle would produce zero torque of the beam, because it is being applied at the axis of rotation. This means we have only two forces acting on the beam, that are actually producing a torque.
So, \Sigma\tau=25N\sin(30^{\circ})\times2.0m-10N\sin(20^{\circ})\times4.0m However, this yields the incorrect value. What did I do wrong?