Net torque about an axis through point A in a massless rod

[paulimerci]

Homework Statement

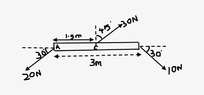
What is the net torque about an axis through point A?

Relevant Equations

Torque = F X d X sin theta

The net torque about an axis through point A is given by,
If I take the axis of rotation perpendicular to the paper and the solution I arrive would be the following below
Net torque = 30 cos45 x 1.5 - 10 cos30X 3
= 5.829Nm ( counterclockwise)

But the book gives an answer like this,
Net torque = 30 cos 45x1.5 - 10 x sin30 x 3 = 16.8Nm.


What did I miss? It looks the horizontal component is perpendicular to the axis of rotation.

 

[kuruman]

The figure does not show where point A is.

 

[paulimerci]

I have updated the figure. Are you able to see it?

 

[Lnewqban]

Are you sure?:
“10 cos30X 3”

 

[paulimerci]

Are you sure?:
“10 cos30X 3”

because cosine component looks perpendicular to the axis of rotation. right?

 

[haruspex]

It looks the horizontal component is perpendicular to the axis of rotation.

But that is not quite the right test. The horizontal component here passes through the axis of rotation, so cannot have any moment about it.
To find the moment a force exerts about an axis, you can either find the perpendicular distance from the line of action of the force to the axis or find the component of the force which is perpendicular to the line joining the point of application to the axis.

See https://www.physicsforums.com/insights/frequently-made-errors-mechanics-moments/

 

[Lnewqban]

because cosine component looks perpendicular to the axis of rotation. right?

 

[haruspex]

View attachment 317297

I think you are not grasping the error @paulimerci is making. It is true that the horizontal component of the 10N is perpendicular to the axis. Indeed, the whole of the 10N is because it lies in the plane perpendicular to the axis. As I wrote in post #6, that is the wrong test.

 

[paulimerci]

But that is not quite the right test. The horizontal component here passes through the axis of rotation, so cannot have any moment about it.
To find the moment a force exerts about an axis, you can either find the perpendicular distance from the line of action of the force to the axis or find the component of the force which is perpendicular to the line joining the point of application to the axis.

See https://www.physicsforums.com/insights/frequently-made-errors-mechanics-moments/

okay if the axis of rotation is along the horizontal component I take the perpendicular component sin theta for 10N. How about 30N force, it looks sin theta perpendicular to the axis of rotation and I cannot use cosine for 30N?

 

[Lnewqban]

I think you are not grasping the error @paulimerci is making. It is true that the horizontal component of the 10N is perpendicular to the axis. Indeed, the whole of the 10N is because it lies in the plane perpendicular to the axis. As I wrote in post #6, that is the wrong test.

Of course, you are correct.
The confusion comes from the different orientation of the angles.
Cosine works for one, but not for the other.

That was the intended hint in my diagram.
Perhaps @paulimerci can graphically see the error in “10 cos30X 3”.

Perpendicular or not to the axis of rotation, a force that has no lever respect to a point is unable to induce any moment on it.

 

[paulimerci]

I still don't get it.

 

[Lnewqban]

I still don't get it.

What are the correct calculated values of the vertical and horizontal components of the 10N force?
Which one is able of induce a moment respect to pivot A?

 

[paulimerci]

I got it right now, I was confused because the text book says cosine for 30 N force. That thing i still don't get it. As @haruspex said "To find the moment a force exerts about an axis, you can either find the perpendicular distance from the line of action of the force to the axis", I did that way and got the answer right.

Net torque at A = (30) (sin45)(1.5) - (10)(sin30)(3) = 16.8Nm

 

[Lnewqban]

I got it right now, I was confused because the text book says cosine for 30 N force. That thing i still don't get it.

What is “that thing”?

 

[paulimerci]

What is “that thing”?

I mean cosine for 30N in the textbook.

 

[haruspex]

the text book says cosine for 30 N force

For the 30N force the angle is 45^o. For that angle, cos and sin have the same value.

 

[paulimerci]

For the 30N force the angle is 45^o. For that angle, cos and sin have the same value.

I understand that but for what reason cosine is used there? What if some other angle was given?

 

[Lnewqban]

Isn't that cosine of 30N the middle vertical force represented and highlighted in the diagram of post #7 above?

 

[paulimerci]

Isn't that cosine of 30N the middle vertical force represented and highlighted in the diagram of post #7 above?

why is it taken as cosine if I take the axis of rotation along x axis? Why I'm not getting it?

 

[Lnewqban]

why is it taken as cosine if I take the axis of rotation along x axis? Why I'm not getting it?

The location and orientation of the angle the force makes with certain reference line is given in the problem, you need to decide which one to use, sine or cosine, according to what projection of the force you need to calculate.

Please, see:
https://www.mathsisfun.com/sine-cosine-tangent.html

http://zonalandeducation.com/mstm/physics/mechanics/forces/forceComponents/forceComponents.html

http://www.mem50212.com/MDME/MEMmods/MEM30005A/add_forces/add_forces.html

 

[haruspex]

I understand that but for what reason cosine is used there? What if some other angle was given?

Look carefully at the diagram. The angle marked as 45° is the angle between the force and the "vertical", whereas the angle marked 30° is between the force and the "horizontal".

 

[paulimerci]

Look carefully at the diagram. The angle marked as 45° is the angle between the force and the "vertical", whereas the angle marked 30° is between the force and the "horizontal".

Which component would you use for 30N? Sine or cosine?

 

[paulimerci]

The location and orientation of the angle the force makes with certain reference line is given in the problem, you need to decide which one to use, sine or cosine, according to what projection of the force you need to calculate.

Please, see:
https://www.mathsisfun.com/sine-cosine-tangent.html

http://zonalandeducation.com/mstm/physics/mechanics/forces/forceComponents/forceComponents.html

http://www.mem50212.com/MDME/MEMmods/MEM30005A/add_forces/add_forces.html

Is this how I have to choose the reference line? see the picture below

 

[haruspex]

Which component would you use for 30N? Sine or cosine?

Call the two marked angles $\alpha=45°$ and $\beta=30°$.
In each case, the line joining the point of application of force to the axis of rotation is horizontal in the diagram, so we want the component of force that's vertical. To find the component in a given direction we use the cosine of the angle between the two.
$\alpha$ is the angle the force makes to the vertical, so we use $\cos(\alpha)=\cos(45°)$.
$\beta$ is the angle the force makes to the horizontal, so we use $\cos(90°-\beta)=\sin(\beta)=\sin(30°)$

 

[paulimerci]

Call the two marked angles $\alpha=45°$ and $\beta=30°$.
In each case, the line joining the point of application of force to the axis of rotation is horizontal in the diagram, so we want the component of force that's vertical. To find the component in a given direction we use the cosine of the angle between the two.
$\alpha$ is the angle the force makes to the vertical, so we use $\cos(\alpha)=\cos(45°)$.
$\beta$ is the angle the force makes to the horizontal, so we use $\cos(90°-\beta)=\sin(\beta)=\sin(30°)$

I really forgot to use this basic trigonometric ratios of complimentary angles. Thank you so much @haruspex ! Now I understand how we get cosine for 30N.

 

[hutchphd]

Am I missing something? The rod is "massless" and is subject to a net force (and torque too) The dynamics might be tricky.

 

[haruspex]

Am I missing something? The rod is "massless" and is subject to a net force (and torque too) The dynamics might be tricky.

Well spotted, but I would guess it is a typo for "massive"

 

[paulimerci]

Well spotted, but I would guess it is a typo for "massive"

No, in the textbook it says massless rod.

 

[haruspex]

No, in the textbook it says massless rod.

Then I guess they just didn’t want the student to add mg.

 

[Lnewqban]

Is this how I have to choose the reference line? see the picture below

Sorry, I have no idea about what you are trying to represent in that picture.

The original question only refers to “the net torque about an axis through point A”.
There is no reference line to represent or discuss, I believe.

Sorry to ask, but how can you be still confused about this problem after studying the links provided in post #20 above?

 

[paulimerci]

I’m not confused, I thought the reference line represents an arbitrary fixed line (as an x-axis or a polar axis) from which coordinates of a point are computed.

 

[Lnewqban]

I’m not confused, I thought the reference line represents an arbitrary fixed line (as an x-axis or a polar axis) from which coordinates of a point are computed.

Sorry, I misunderstood your picture.

 

[topsquark]

I’m not confused, I thought the reference line represents an arbitrary fixed line (as an x-axis or a polar axis) from which coordinates of a point are computed.

Another way to look at the angle problem is to write the torque equation as $\tau = \textbf{F} \times \textbf{d}$. The magnitude of the torque will be $\tau = F d ~ sin( \theta )$ where the angle is between and measured counterclockwise. To do this draw a quick sketch and place the tails of d and F at the same point.

-Dan

 

[paulimerci]

I’m not confused, I thought the reference line represents an arbitrary fixed line (as an x-axis or a polar axis) from which coordinates of a

Sorry, I misunderstood your picture.

View attachment 317371

Thank you!