- #1
ysk1
- 32
- 1
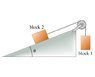
(Please look at the diagram attached at the bottom)
Question:
Newton's 2nd law, F=ma, is a vector equation. To add or subtract vectors it is often easiest to decompose the vector into components. Whereas a particular set of vector components is only valid in a particular coordinate system, the vector equality holds in any coordinate system, giving you freedom to pick a coordinate system that most simplifies the equations that result from the component equations.
It's generally best to pick a coordinate system with as many unknowns as possible along the coordinate axes. Vectors that lie along the axes appear in only one of the equations for each component, rather than in two equations with trigonometric prefactors. Note that it is sometimes advantageous to use different coordinate systems for each body in the problem.
In this problem, you should use Cartesian coordinates and your axes should be stationary with respect to the inclined plane.
Given the criteria just described, what orientation of the coordinate axes should you use in this problem?
In the answer options, "tilted" means with the x-axis oriented parallel to the plane (i.e., at angle theta to the horizontal), and "level" means with the x-axis horizontal.
1.
A) tilted for both block 1 and block 2
B) tilted for block 1 and level for block 2
C) level for block 1 and tilted for block 2
D) level for both block 1 and block 2
2. What is the sum of the x components of the forces acting on block 2? Take forces acting up the incline to be positive.
Express your answer in terms of some or all of the variables tension T, m_2, the magnitude of the acceleration of gravity g, and theta.
I don't get what these questions are asking, especially question 1.
Because I'm stuck on question 1, I can't proceed to question 2.
The question doesn't even explain what Cartesian coordinates are. :(
Could anyone please tell me how I should do these problems.
Thank you.
Question:
Newton's 2nd law, F=ma, is a vector equation. To add or subtract vectors it is often easiest to decompose the vector into components. Whereas a particular set of vector components is only valid in a particular coordinate system, the vector equality holds in any coordinate system, giving you freedom to pick a coordinate system that most simplifies the equations that result from the component equations.
It's generally best to pick a coordinate system with as many unknowns as possible along the coordinate axes. Vectors that lie along the axes appear in only one of the equations for each component, rather than in two equations with trigonometric prefactors. Note that it is sometimes advantageous to use different coordinate systems for each body in the problem.
In this problem, you should use Cartesian coordinates and your axes should be stationary with respect to the inclined plane.
Given the criteria just described, what orientation of the coordinate axes should you use in this problem?
In the answer options, "tilted" means with the x-axis oriented parallel to the plane (i.e., at angle theta to the horizontal), and "level" means with the x-axis horizontal.
1.
A) tilted for both block 1 and block 2
B) tilted for block 1 and level for block 2
C) level for block 1 and tilted for block 2
D) level for both block 1 and block 2
2. What is the sum of the x components of the forces acting on block 2? Take forces acting up the incline to be positive.
Express your answer in terms of some or all of the variables tension T, m_2, the magnitude of the acceleration of gravity g, and theta.
I don't get what these questions are asking, especially question 1.
Because I'm stuck on question 1, I can't proceed to question 2.
The question doesn't even explain what Cartesian coordinates are. :(
Could anyone please tell me how I should do these problems.
Thank you.
Attachments
Last edited: