Jtwa
- 9
- 0
1. Homework Statement
h = 17.2 cm
A = 12.32cm2
E = 410 MPA
Fapp = 6130 N
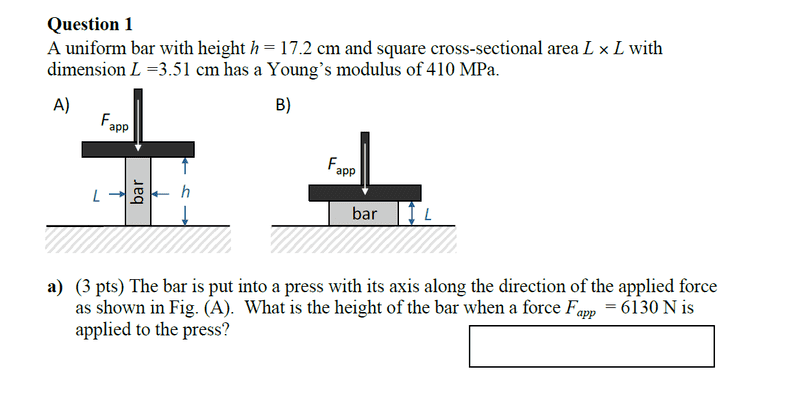
2. Homework Equations
Stress
σ = F/A where F is force applied and A is cross sectional area of side where force is applied
Strain
ε = ΔL/L where L is the length of the bar and ΔL is the change of length of bar
Young's Modulus
E = stress/strain = FL/AΔL
3. My attempt at solution
We are solving first solving for ΔL which I got as 0.864cm and then we subtract that from 17.2cm which I got as 16.34cm
I'm not sure if my thought process is correct or how to approach this question. What is Young's modulus ? Am I approaching the problem correctly? Am I looking for the right variable? Did I get the correct answer ? Just need reassurance. Thanks in advance guys!
h = 17.2 cm
A = 12.32cm2
E = 410 MPA
Fapp = 6130 N
2. Homework Equations
Stress
σ = F/A where F is force applied and A is cross sectional area of side where force is applied
Strain
ε = ΔL/L where L is the length of the bar and ΔL is the change of length of bar
Young's Modulus
E = stress/strain = FL/AΔL
3. My attempt at solution
We are solving first solving for ΔL which I got as 0.864cm and then we subtract that from 17.2cm which I got as 16.34cm
I'm not sure if my thought process is correct or how to approach this question. What is Young's modulus ? Am I approaching the problem correctly? Am I looking for the right variable? Did I get the correct answer ? Just need reassurance. Thanks in advance guys!
Last edited: