SUMMARY
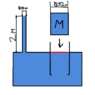
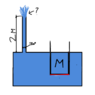
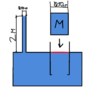
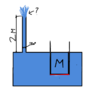
The discussion centers on Archimedes' principle and the behavior of water displacement when a smaller container is lowered onto a movable platform in a large container of water. It concludes that the volume of displaced water will equal the volume of the smaller container, provided that the system is properly configured and the pressure from the water column is accounted for. The resistance created by the height of the water column does not affect the volume displaced, as the incompressibility of water ensures consistent displacement under pressure. Clarification on the mass of the piston and its ability to maintain the water column height is essential for accurate analysis.
PREREQUISITES
- Understanding of Archimedes' principle
- Basic knowledge of fluid mechanics
- Familiarity with pressure concepts in fluids
- Ability to interpret diagrams of fluid systems
NEXT STEPS
- Research the implications of fluid incompressibility in practical applications
- Explore the relationship between pressure and volume in fluid dynamics
- Study the mechanics of movable platforms in fluid systems
- Examine case studies involving Archimedes' principle in engineering
USEFUL FOR
Students of physics, engineers working with fluid systems, and anyone interested in the practical applications of Archimedes' principle in real-world scenarios.