Femme_physics
Gold Member
- 2,548
- 1
Homework Statement
http://img823.imageshack.us/img823/3720/thisonev.jpg
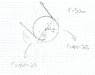
I just want to know if my horizontal distances of T when I calculate moments are correct (I need to add a certain length to 250, and reduce the same length from 250 - I believe. I only solved for that distance you need to add and reduce. I think that once I got that I can solve the question fully.
The Attempt at a Solution
Attached.
Attachments
Last edited by a moderator: