squenshl
- 468
- 4
Homework Statement
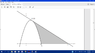
Calculate the area between ##y = -x^2+3x+10## and ##y = -x+14##. Note that ##y = -x+14## is the tangent to the curve ##y = -x^2+3x+10## at the point ##(2,12)##.
Homework Equations
The Attempt at a Solution
Is it as simple as calculating ##\int_{5}^{14} -x+14+x^2-3x-10 = \int_{5}^{14} x^2-4x-10##?