Area between two eccentric circles

[agordon]

Hi, here is my geometry problem.

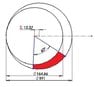
I have two circles, one inside the other. The larger diameter is denoted by D, and the smaller by d. Their centers are eccentric by a distance e. Now, there is a line from the center of the smaller circle to the outside of the larger circle. I have derived an equation for the length of those lines at any given angle from the horizontal. It is:

x = e*cos(a) + 0.5*sqrt(D^2 - 4*e^2*sin^2(a)).

I hope that makes sense, I'm not sure how to write equations on this forum.

So now, there is another line, 60 degrees from the first line. There is an area bounded by the two lines and the two circles. Can anyone figure out how to find this area? The attachment shows the situation I am talking about. The area colored red is the area in question.

Thanks,
AGordon

 

[agordon]

Well I may have figured it out. At least found a step toward the solution. I realized that the equation I had for the distance from the center of the small diameter to the outside of the large diameter was the equation of a circle in polar coordinates. So if I can integrate that equation from a to a+60 degrees that will give me the area of the un-centered pie section. Then the area in question is that minus the area of the small diameter pie.

So anyways, I am very rusty on my calculus so anyone who can help integrate an equation in polar coordinates please help.

Thanks!