dluu
- 15
- 0
Hi,
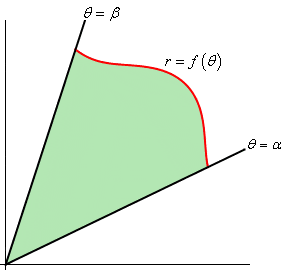
I'm trying to find the area of a segment of a circle that is not at the origin. It will look similar to this picture below but I need to find the area enclosed by a circle.
Using the polar equation of a circle provided by wikipedia:
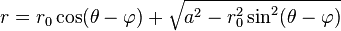
and integrating to find the area of a curve:
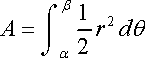
Resulting in:
http://desmond.imageshack.us/Himg145/scaled.php?server=145&filename=equation.png&res=landing
Am I on the right track or is there a more simple way? I'm not sure how to integrate this kind of function. I tried and got so lost.
I'm trying to find the area of a segment of a circle that is not at the origin. It will look similar to this picture below but I need to find the area enclosed by a circle.
Using the polar equation of a circle provided by wikipedia:
and integrating to find the area of a curve:
Resulting in:
http://desmond.imageshack.us/Himg145/scaled.php?server=145&filename=equation.png&res=landing
Am I on the right track or is there a more simple way? I'm not sure how to integrate this kind of function. I tried and got so lost.
Last edited by a moderator: