Solving Astronaut Problem: Force & Acceleration

  • Thread starter Thread starter fashion_fever
  • Start date Start date
  • Tags Tags
    Astronaut
AI Thread Summary
Three astronauts are pushing a 127 kg satellite in space using jetpacks, applying three different forces at various angles. The total force needs to be calculated by resolving each force into its horizontal and vertical components. The initial attempt at solving the problem involved incorrect signs for the forces, particularly in the horizontal direction. After clarification, the correct approach was to ensure that opposing forces were accurately represented in the calculations. The discussion concludes with the user successfully finding the correct acceleration after addressing the sign errors in their equations.
fashion_fever
Messages
12
Reaction score
0

Homework Statement



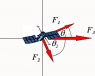
Three astronauts equipped with jetpacks are pushing a satellite, having a mass of 127 kg, through space. The forces being exerted on the satellite are F1=31.7 N at an angle of 30.8 degrees above the horizontal, F2=40.2 N at 58.6 degrees below the horizontal, and F3=53.9 N along the horizontal.

What is the magnitude of the satellite's acceleration?


Homework Equations



okay so i thought of finding the total force and then using f=ma.

The Attempt at a Solution



31.7N : 31.7sin30.8, 31.7cos30.8
40.2N: -40.2sin58.6, -40.2cos58.6
53.9N: 53.9sin0, 53.9cos0

i added the sin together and cos together and used Pythagorean Theorem to find the total force and plug that into the equation and i got the answer wrong so i don't know where it's wrong. Plz help..
 

Attachments

  • hr-pic0510.png
    hr-pic0510.png
    5.1 KB · Views: 467
Physics news on Phys.org
What answer did you get? I've worked it out and will compare yours to mine.

Jared
 
Here's a hint, the vertical velocities are opposing each other so one is + and one is - (Sin values are correct). Your problem is you have also made your equation so that the horizontal force of the lower guy (below horizontal) is opposing the other two.

Jared
 
Last edited:
oh! omg..okay i got it it was suppose to be +40.2cos58.6..
tytytytyty!
 
There we go, glad to help.

Jared
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Three astronauts equipped with jetpacks
Replies
4
Views
2K
Equilibrium of Forces and Torques on Sawhorses Supporting a Person on a Board
Replies
6
Views
2K
Astronaut in space, calculating velocity etc
Replies
12
Views
5K
Solving the Spacewalking Astronaut Problem
Replies
1
Views
2K
What is the distance between the astronaut and the satellite after 1.0 min?
Replies
2
Views
19K
Calculating total Coulomb force vector ?
Replies
1
Views
2K
Astronaut Acceleration Question
Replies
1
Views
3K
Solving Cart Force Question: Magnitude & Direction
Replies
21
Views
7K
Basic Newton's Laws and Applied Force: 3 boxes
Replies
5
Views
8K
Calculating Acceleration: 3 Astronauts, 120kg Asteroid & Jetpacks
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top