Lambda96
- 233
- 77
- Homework Statement
- Use the expression for the Planck function in the Rayleigh-Jeans approximation and estimate to which frequencies it can be used to determine the temperature of an astronomical source of temperature 20 K. Use the first two terms in the Taylor-series from the lecture and assume 10% relative accuracy.
- Relevant Equations
- T-h*f/2*k T=Temperature, h=Planck constant, f=Frequency , k=Boltzmann constant
Hi,
I am not quite sure if I have calculated the homework correctly :-)
I proceeded in such a way that I first calculated from which frequency the two terms are equal, and thus the equation results in zero.
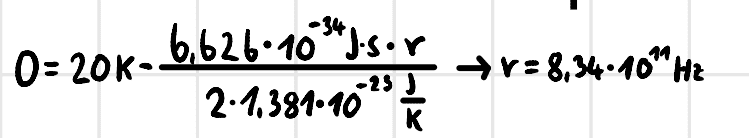
Then I figured a relative accuracy of 10% equals a relative error of 90%. So I calculated at which frequency I have a relative error of 90% and exactly this frequency is the one I am looking for.
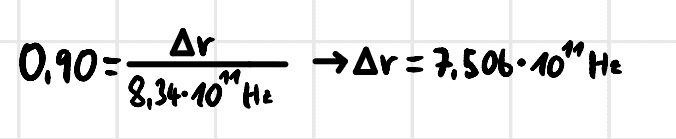
Am I thinking correctly, or am I completely wrong? :-)
I am not quite sure if I have calculated the homework correctly :-)
I proceeded in such a way that I first calculated from which frequency the two terms are equal, and thus the equation results in zero.
Then I figured a relative accuracy of 10% equals a relative error of 90%. So I calculated at which frequency I have a relative error of 90% and exactly this frequency is the one I am looking for.
Am I thinking correctly, or am I completely wrong? :-)