Atwood machine with two holes in pulley.

In summary, the conversation discusses a system consisting of a pulley and two masses, and finding the angular acceleration of the pulley. The equations used are L=T-U and I=I_{cm}+mh^{2}. The solution is attached and the person is interested in knowing if their calculation for the moment of inertia is correct.
  • #1
AbigailM
46
0

Homework Statement


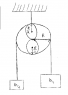
A system consists of a pulley and two masses m1, m2 haning from it as shown in the figure. The pulley is a disk of radius R with constant mass density that has two circular hole with radius R/2. Find the angular acceleration of the pulley.

Figure attached.


Homework Equations


L=T-U
[itex]I=I_{cm}+mh^{2}[/itex]

The Attempt at a Solution


The solution is attached.

I'm not interested in knowing if my calculation for the moment of inertia is correct which is found at the bottom of the solution.
 

Attachments

  • atwood.png
    atwood.png
    10.9 KB · Views: 506
  • F10-5sol.jpg
    F10-5sol.jpg
    27.6 KB · Views: 497
Physics news on Phys.org
  • #2
In the first equation for I at the bottom of the page, shouldn't the last term be negative? (Never mind, I missed seeing a set of parentheses!)

It all looks good to me.
 
  • #3
Ooops I made a typo. I meant to say that I'm interested in knowing whether or not my moment of inertia is correct.

Oh cool TSny you read it how I meant it.
 

Related to Atwood machine with two holes in pulley.

1. What is an Atwood machine with two holes in the pulley?

An Atwood machine with two holes in the pulley is a simple mechanical device used to demonstrate the principles of acceleration and forces. It consists of a pulley with two holes, two masses of unequal weight, and a string connecting the masses over the pulley.

2. How does an Atwood machine with two holes in the pulley work?

The Atwood machine with two holes in the pulley works by utilizing the difference in weight between the two masses to create a net force, causing the system to accelerate. As one mass falls, it pulls the other mass up, creating a tension in the string and an acceleration in the direction of the heavier mass.

3. What is the purpose of having two holes in the pulley for an Atwood machine?

Having two holes in the pulley allows for the string to be attached at different points, creating different configurations and changing the direction of the net force. This allows for the demonstration of different concepts, such as the effect of changing the direction of the net force on the acceleration of the system.

4. How does the mass and weight of the two masses affect the motion of an Atwood machine with two holes in the pulley?

The mass and weight of the two masses play a crucial role in determining the acceleration of the system. The heavier mass will experience a greater force of gravity, causing it to accelerate faster, while the lighter mass will accelerate slower. This difference in acceleration creates the net force that causes the motion of the system.

5. What are the real-world applications of an Atwood machine with two holes in the pulley?

An Atwood machine with two holes in the pulley is commonly used in physics demonstrations and experiments to illustrate the principles of forces and acceleration. It also has practical applications in engineering, such as in elevators and cranes, where pulley systems are used to lift heavy objects using a minimal amount of force.

Similar threads

What is the acceleration of the masses in a double double Atwood machine?
Replies
2
Views
2K
Lagrange EQ for a Double Atwood Machine
Replies
8
Views
9K
Lagrangian equation for 5 pulley Atwood Machine.
Replies
4
Views
6K
How Do You Calculate Tensions and Accelerations in a Modified Atwood Machine?
Replies
1
Views
2K
Lagrangian of two masses connected by a pulley on inclined p
Replies
2
Views
4K
Atwood machine mass accleration problem
Replies
1
Views
4K
Find acceleration of a modified atwood machine
Replies
1
Views
8K
Atwood machine with variable mass
Replies
7
Views
3K
Angular acceleration of an atwood pulley
Replies
8
Views
3K
Double Atwood Machine: relation between the contraints & the variables ?
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top