Poetria
- 267
- 42
Homework Statement
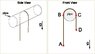
A rope of uniform mass density is passed above the top of a fixed pipe of circular cross section.
Points B and C - the points where the rope loses contact with the pipe.
Points A and D - at the ends of the rope
The length of the segment AB = 2d
The length of the segment CD = d.
The magnitude of the force of tension at the point A - ?
The magnitude of the force of tension at the point D - ?
I have calculated the ratio: tension at the point B over tension at the point C = 2
The Attempt at a Solution
[/B]
I thought tension at A = 2
tension at D = 1
Well, this is wrong. I am missing something.
It is somewhat similar to a simple Atwood machine, isn't it?